A seris LR circuit is connected to a voltage source with . After very large time, current 1(t) behaves as
:



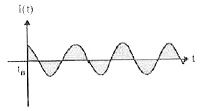
The correct Answer is:D
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (TOPIC 1: Alternating Current, Voltage and Power)
20 Videos
- ALTERNATING CURRENT BOOK - DISHA PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - Exercise - 1 : CONCEPT BUILDER (Topic 2: A.C Circuits and Power Factor)
31 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
Similar Questions
A series R-L circuit is subjected to an alternating voltage given as (v=v0sinωt). Then the variation of peak current (i) with frequency (v) is denoted by
View SolutionIn the circuit shown the source voltage is given asv=V0 sin ωt. Find the current through the source as a function of time.
View Solution
Knowledge Check
A series LR circuit is connected to a voltage source with V(t) = V0 sin ω t. after very large time, current I(t) behaves as (t0>>LR)
A B
B C
C D
D
A capacitor of capacity C is connected in A.C circuit. If the applied emf is V=V0sinωt, then the current is
AI=V0LωsinωtBI=V0ωCsin(ωt+π2)CI=V0CωsinωtDt=V0Cωsin(ωt+π2)A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent l(t) leads voltage V(t) by 180∘BCurrent l(t) lags voltage V(t) by 90∘COver a full cycle the capacitor C does not consume any energy from the voltage sourceDCurrent l(t) is in phase with voltage V(t)
Figure shows a series LCR cicuit connected to a variable voltage source V=10sin(ωt+π/4),xL=10Ω,Xc=6Ω,R=3Ω
Calculate Z,i0,irms,Vrms,VLO,VCO,VRO,β,VLRms,VCRms,VRms,i(t),VL(t),Ve(t), and VR(t)
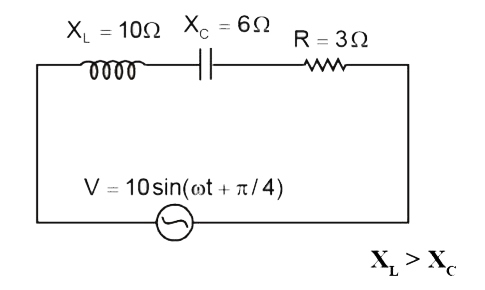
View SolutionA coil with active resistance R and inductance L was connected at the moment t=0 to a source of voltage V=Vmcosωt. Find the current in the coil as a function of time t.
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionA circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View Solution
