A series R-L circuit is subjected to an alternating voltage given as (v=v0sinωt). Then the variation of peak current (i) with frequency (v) is denoted by
To solve the problem of finding the variation of peak current (I) with frequency (ω) in a series R-L circuit subjected to an alternating voltage v=V0sin(ωt), we can follow these steps:
Step 1: Write the Kirchhoff's Law Equation
For a series R-L circuit, according to Kirchhoff's law, we can write:
Ldidt+Ri=V0sin(ωt)
Step 2: Rearrange the Equation
Rearranging the equation gives:
Ldidt=V0sin(ωt)−Ri
Dividing the entire equation by L:
didt−RLi=V0Lsin(ωt)
Step 3: Solve the Differential Equation
To solve this first-order linear differential equation, we can use an integrating factor:
e−RLt
Multiplying through by the integrating factor:
e−RLtdidt−RLe−RLti=V0Le−RLtsin(ωt)
This simplifies to:
ddt(ie−RLt)=V0Le−RLtsin(ωt)
Step 4: Integrate Both Sides
Integrating both sides from 0 to t:
ie−RLt=∫t0V0Le−RLtsin(ωt)dt+C
Where C is the constant of integration.
Step 5: Evaluate the Integral
The integral can be evaluated using integration by parts or a known formula:
∫e−αtsin(βt)dt=βe−αtsin(βt)+αe−αtcos(βt)α2+β2
Applying this to our integral, we find:
i(t)=V0L⋅ωe−RLtsin(ωt)+RLe−RLtcos(ωt)R2+ω2L2
Step 6: Find the Peak Current
The peak current I0 can be expressed as:
I0=V0√R2+(ωL)2
This shows that the peak current I0 varies with frequency ω.
Step 7: Analyze the Variation
As ω increases, the term ωL increases, thus affecting the denominator √R2+(ωL)2 and consequently decreasing the peak current I0.
Final Expression
The final expression for the peak current as a function of frequency is:
I0=V0√R2+(ωL)2
For a series R-L circuit, according to Kirchhoff's law, we can write:
Ldidt+Ri=V0sin(ωt)
Rearranging the equation gives:
Ldidt=V0sin(ωt)−Ri
Dividing the entire equation by L:
didt−RLi=V0Lsin(ωt)
To solve this first-order linear differential equation, we can use an integrating factor:
e−RLt
Multiplying through by the integrating factor:
e−RLtdidt−RLe−RLti=V0Le−RLtsin(ωt)
This simplifies to:
ddt(ie−RLt)=V0Le−RLtsin(ωt)
Integrating both sides from 0 to t:
ie−RLt=∫t0V0Le−RLtsin(ωt)dt+C
Where C is the constant of integration.
The integral can be evaluated using integration by parts or a known formula:
∫e−αtsin(βt)dt=βe−αtsin(βt)+αe−αtcos(βt)α2+β2
Applying this to our integral, we find:
i(t)=V0L⋅ωe−RLtsin(ωt)+RLe−RLtcos(ωt)R2+ω2L2
The peak current I0 can be expressed as:
I0=V0√R2+(ωL)2
This shows that the peak current I0 varies with frequency ω.
As ω increases, the term ωL increases, thus affecting the denominator √R2+(ωL)2 and consequently decreasing the peak current I0.
The final expression for the peak current as a function of frequency is:
I0=V0√R2+(ωL)2
Topper's Solved these Questions
Similar Questions
In a series LCR circuit connected to an ac source of variable frequency and voltage v=vmsinωt, draw a plot showing the variation of current (I) with angular frequency (ω) for two different values of resistance R1andR2(R1>R2). Write the condition under which the phenomenon of resonance occurs. For which value of the resistance out of the two curves, a sharper resonance is produced ? Define Q-factor of the circuit and give its significance.
View SolutionThe average value of an alternating voltage V=V0sinωt over a full cycle is
View SolutionThe average value of an alternating voltage V=V0sinωt over a full cycle is
View SolutionIn the given figure , a series L-C-R circuit is connected to a variable frequency source of 230 V . The impedance and amplitude of the current at the resonating frequency will be
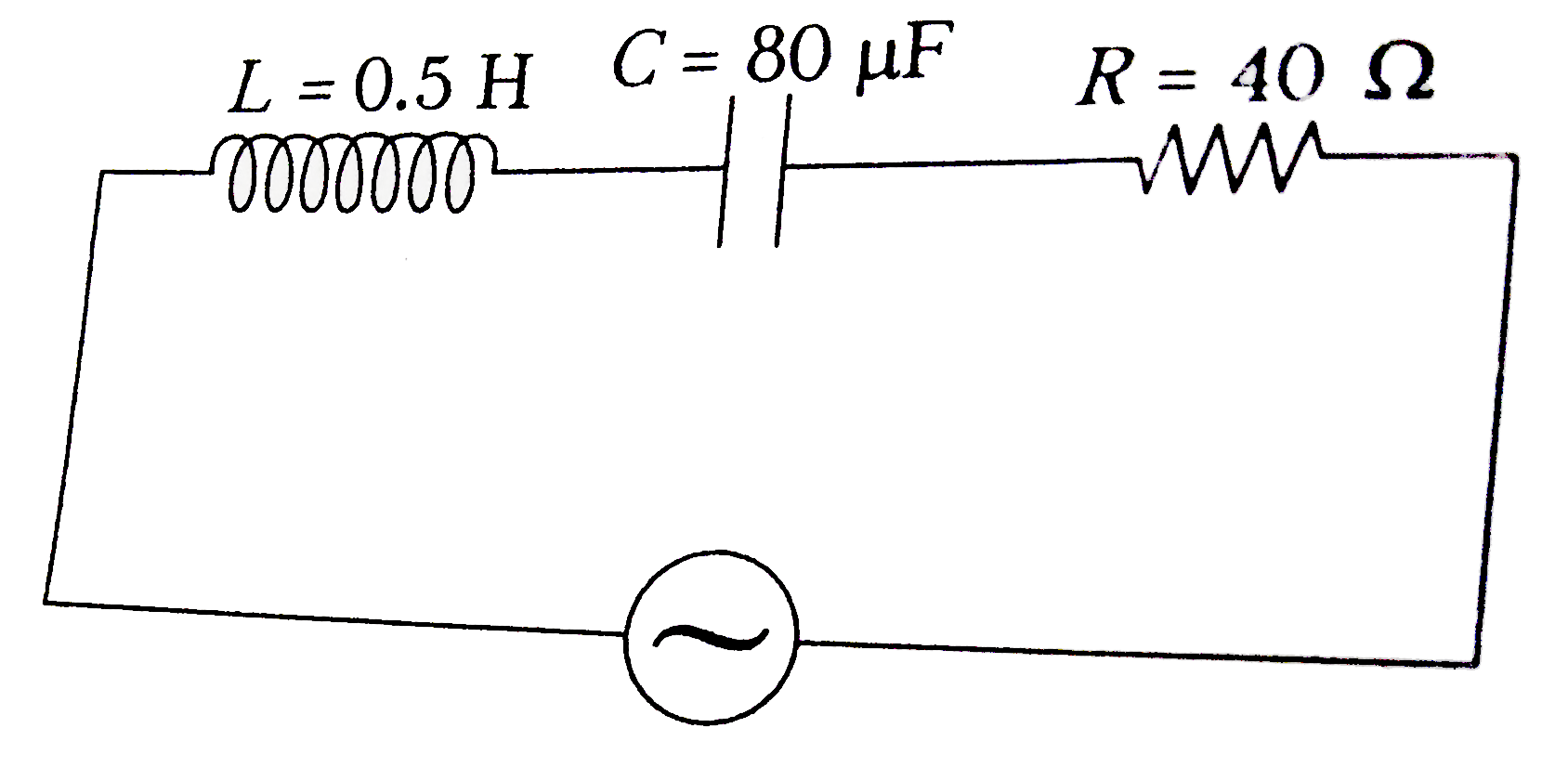
View SolutionA coil of inductance 5.0 mH and negligible resistance is connected to an alternating voltage V=10sin(100t). The peak current in the circuit will be:
View SolutionThe alternating current in a circuit is given by I=50sin314t. The peak value and frequency of the current are
View SolutionA circuit contains resistance R and an inductance L in series. An alternating voltage V=V0sinωt is applied across it. The currents in R and L respectively will be
 .
.
View SolutionA circuit contains resistance R and an inductance L in series. An alternating voltage V=V0sinωt is applied across it. The currents in R and L respectively will be
 .
.
View SolutionA circuit conatining of a capacitor and an active resistance R=110Ω connected in series is fed and alternating voltage with amplitudeV0=110V . In this case, the amplitude of current is equal to I0=0.50A. Find the phase difference between the current and the voltage fed .
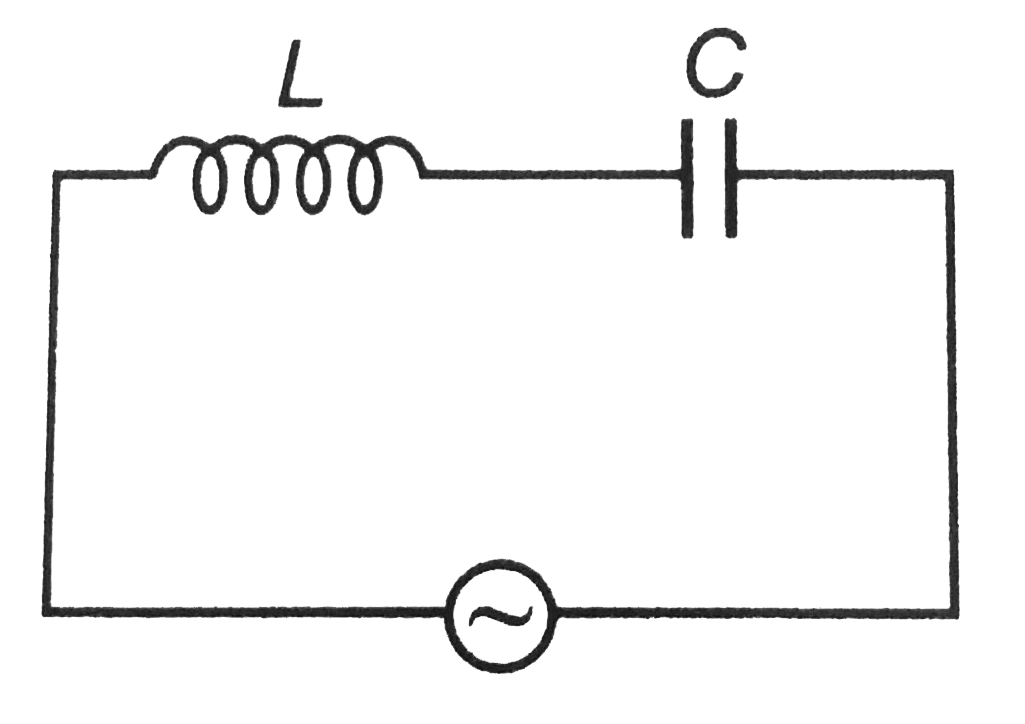
View SolutionIn a series L−C circuit, the applied voltage is V0. if omega is very low, then the voltage drop across the inductor VL and capacitor VC are
 .
.
View Solution




