For the LCR circuit, shown here, the current is observed to lead the applied voltage. An additional capacitor C', when joined with the capacitor C present in the circuit, makes the power factor of the circuit unity. The capacitor C' must have been connected in:
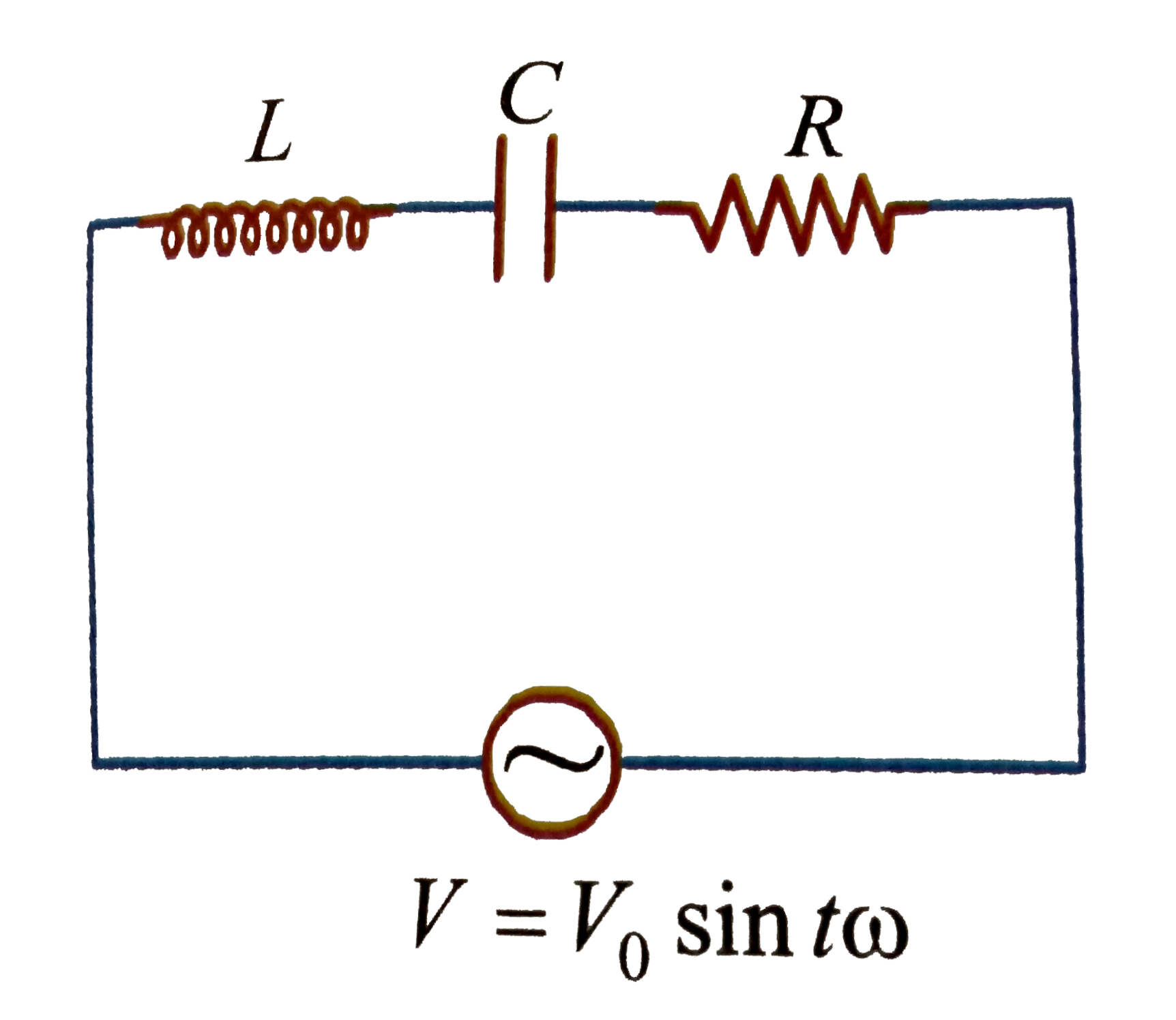
series with C and has a magnitude Cω2LC−1
series with C and has a magnitude 1−ω2LCω2L
parallel with C and has a magnitude 1−ω2LCω2L
parallel with C and has a magnitude Cω2LC−1
The correct Answer is:C
Power factor
cosϕ=R√R2+[ωL−1ω(C+C.)]2=1
On solving we get,
ωL=1ω(C+C.)
C.=1−ω2LCω2L
Here option (c) is the correct answer.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:DISHA PUBLICATIONChapter:ALTERNATING CURRENT Exercise:Exercise - 1 : CONCEPT BUILDER (TOPIC 1: Alternating Current, Voltage and Power)
Explore 20 Videos
- ALTERNATING CURRENT Book:DISHA PUBLICATIONChapter:ALTERNATING CURRENT Exercise:Exercise - 1 : CONCEPT BUILDER (Topic 2: A.C Circuits and Power Factor)
Explore 31 Videos
- ATOMSBook:DISHA PUBLICATIONChapter:ATOMSExercise:EXERCISE-2: CONCEPT APPLICATOR
Explore 30 Videos
Similar Questions
(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?

(ii) What making any other change, find the value of the additional capacitor C, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
View SolutionWhat is the power factor of an A circuit containing inductor or capacitor ?
View Solution
Knowledge Check
The power factor of LCR a.c. circuit at resonance is
A1√2B1CzeroD12In the circuit shown in the figure, the total charge is 750μC and the voltage across capacitor C2 is 20 V. Then the charge on capacitor C2 is:
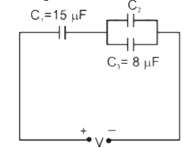 A650μCB450μCC590μCD160μC
A650μCB450μCC590μCD160μCThree capacitor A,B, and C, are connected in a circuit as shown in. What is the charge in μC on the capacitor B?
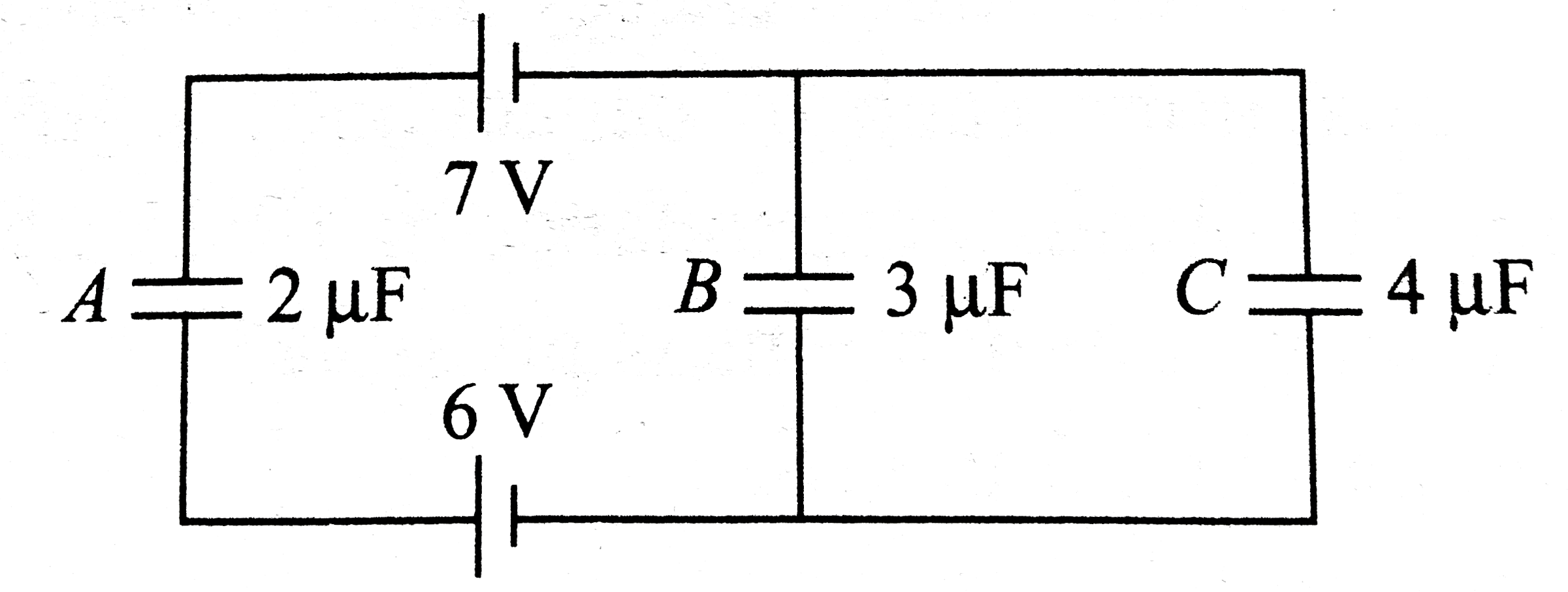 .A1/3B2/3C1D4/3
.A1/3B2/3C1D4/3
In the circuit shown here, at the steady state, the charge on the capacitor is
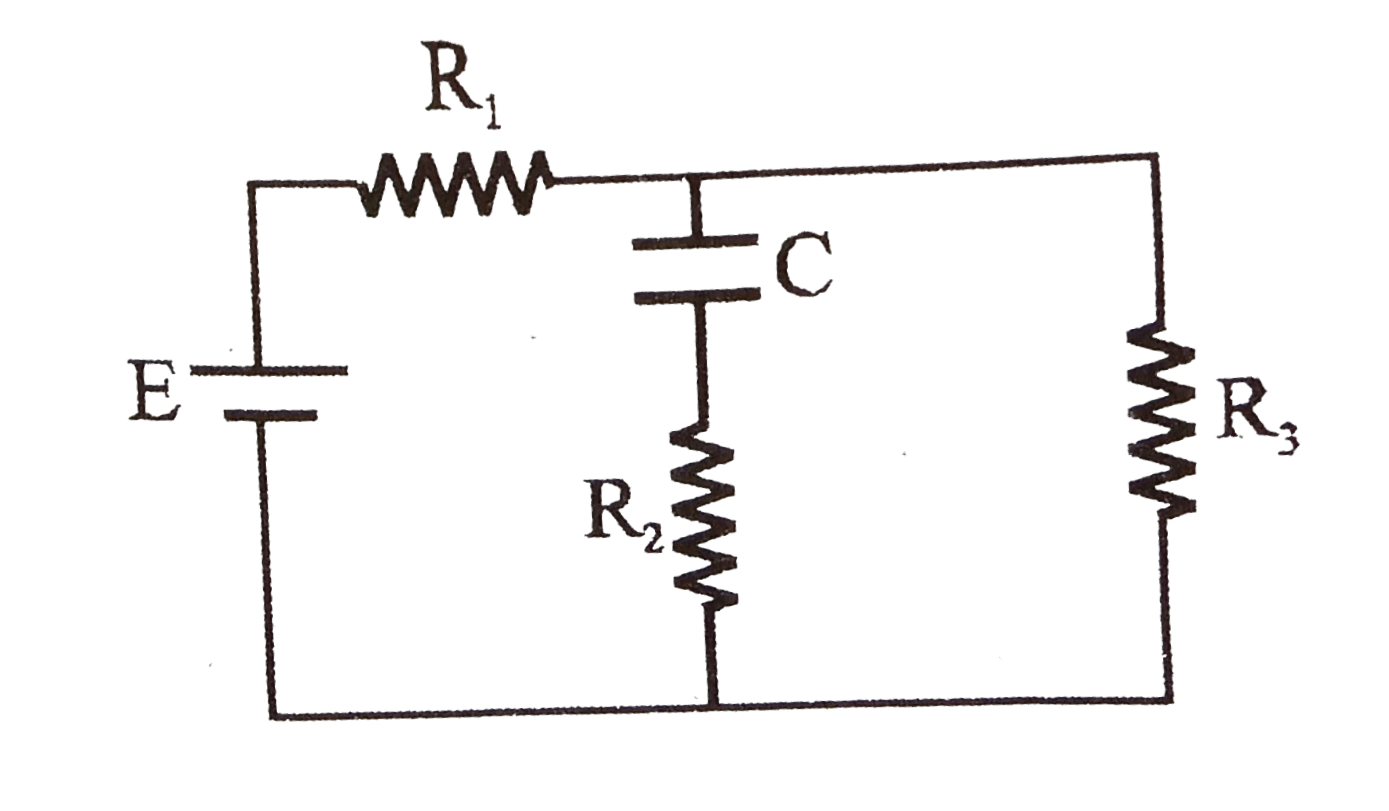
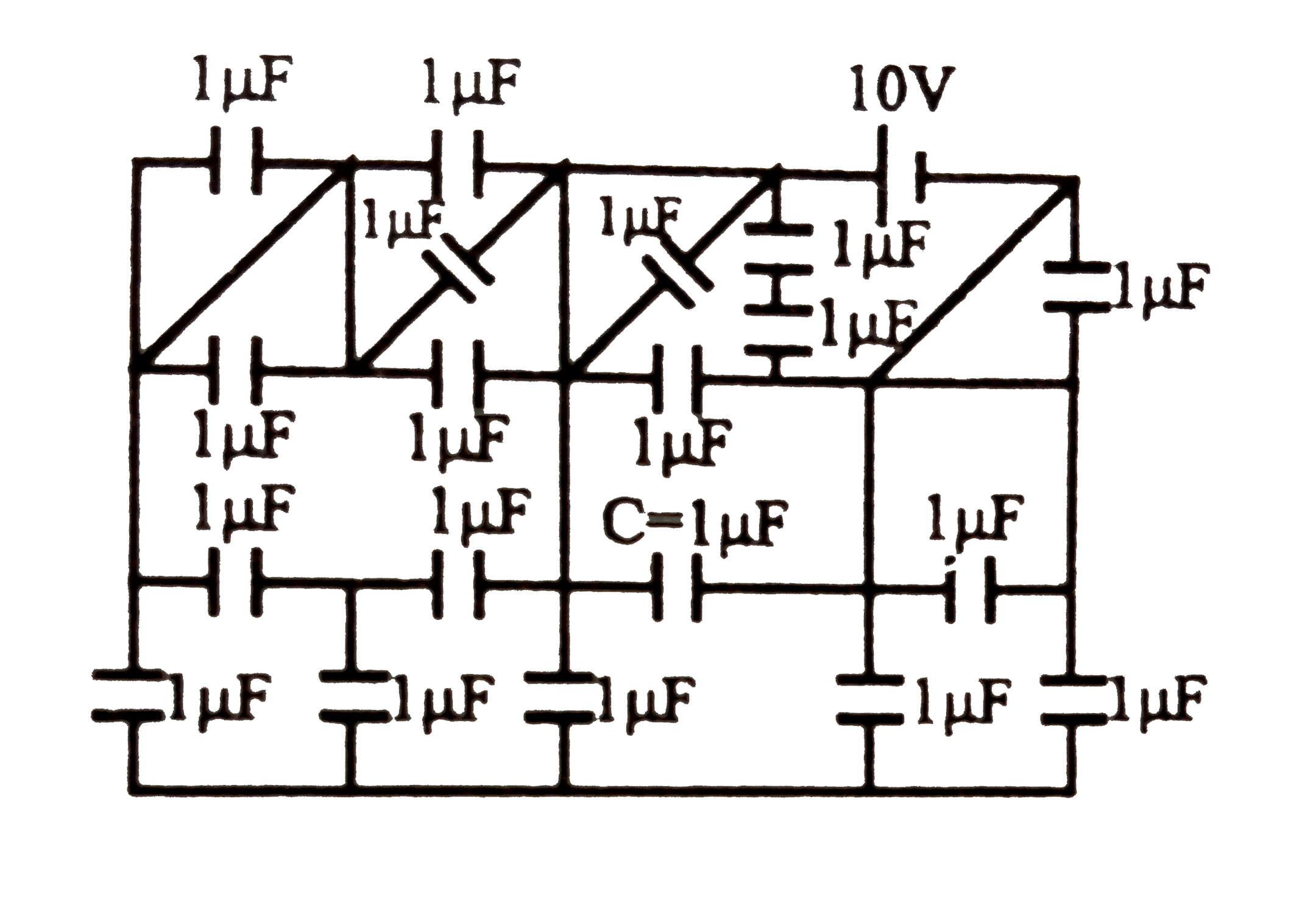
View SolutionFind the charge on the capacitor C=1μF in the circuit shown in the figure.
View Solution(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?

(ii) What making any other change, find the value of the additional capacitor C, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
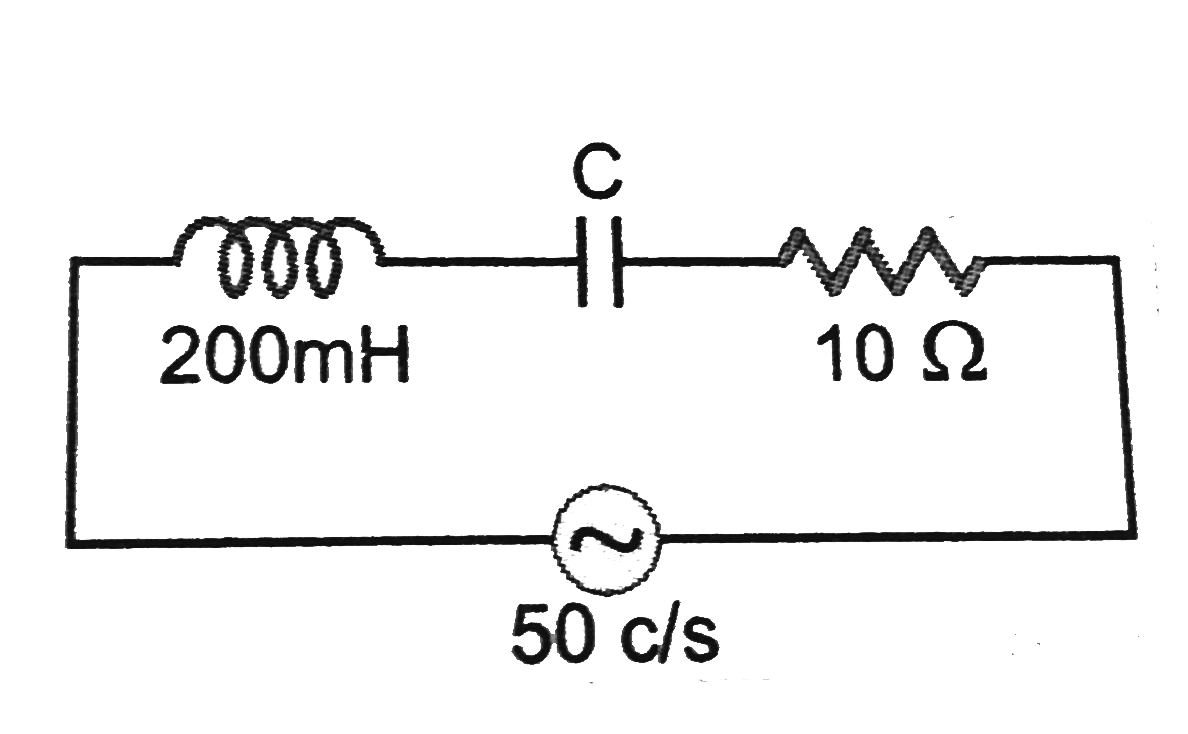
View SolutionIn the circuit shown in fin. Calculate the capacitance C of the capacitor, if the power factor of the circuit is unity. Also, calculate Q factor of the circuit.
View Solution
The current in the LCR circuit shown in the figure is observed to lead the voltage in phase. Without making any other change in the circuit, a capacitor, of capacitance C0 is (appropriately) joined to the capacitor C. This results in making the current, in the joined to the capacitor C. This results in making the current, in the modified' circuit, flow in phase with the applied voltage.
Draw a diagram of the modified circuit and obtain an expression of C0 in terms of Ω, L and C.
View Solution
