The largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
Step by step video & image solution for The largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e^(-x^2) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The area of the area bounded by the curve y = log x - axis and the side x = e is
View SolutionA rectangle has one side on the positive side of Y - axis and one side on the positive side of X - axis. The upper right hand vertiex is on the curve y=logxx2. The maximum area of the rectangle is ………. sq. unit.
View Solutionआयत जिसका आधार x-अक्ष पर तथा इसके दो शीर्ष वक्र y=e−x2 पर स्थित है, का अधिकतम क्षेत्रफल ज्ञात कीजिए |
View Solutionकिसी आयत की एक भुजा धनात्मक y-अक्ष पर और एक धनात्मक x-अक्ष पर है। आयत का ऊपरी दायी और का शीर्ष वक्र y=lnxx2 पर स्थित है, तब आयत का अधिकतम क्षेत्रफल होगा
View SolutionFind the area of the largest rectangle in the first quadrant with two sides on x-axis and y-axis and one vertex on the curve y=12−x2
View Solutionवक्र y=2x4−x2,x− अक्ष और वक्र के दो निम्नष्टो की कोटियों के बीच का क्षेत्रफल है
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (-2,1) and (2,4). Then the area of the rectangle is
View SolutionFour particles, each with mass m are arranged symmetrically about the origin on the x axis. A fifth particle, with mass M, is on the y axis. The direction of the gravitational force on M is:
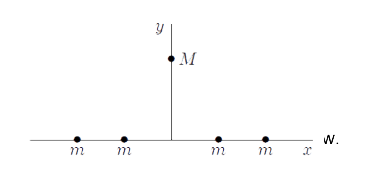
View Solution
