Find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12−x2.
Step by step video & image solution for Find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12-x^2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionThe largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionThe largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionFind the area of the largest rectangle in the first quadrant with two sides on x-axis and y-axis and one vertex on the curve y=12−x2
View SolutionThe maximum area of a rectangle whose two vertices lie on the x-axis and two on the curve y=3−|x|,−3≤x≤3
View SolutionThe area (in sq. units) of the largest rectangle ABCD whose vertices A and B lie on the x - axis and vertices C and D lie on the parabola, y=x2−1 below the x - axis, is :
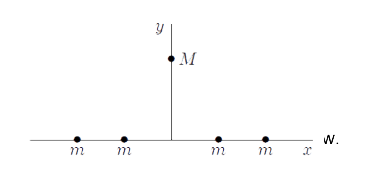
View SolutionFour particles, each with mass m are arranged symmetrically about the origin on the x axis. A fifth particle, with mass M, is on the y axis. The direction of the gravitational force on M is:
 View Solution
View SolutionMaximum area of rectangle whose two vertices lie on the x -axis and two on the curve y=4−|x| ∀|x|<4 is
View SolutionFind the area bounded by the curves y=x+√x2andxy=1, the x-axis and the line x=2.
View SolutionFind the area of the region bounded by the curve y=x2 , the X−axis and the given lines x = 0 , x = 3
View Solution

