A coin is placed on the horizontal surface of a rotation disc. The distance of the coin from the axis is 1 m and coefficient of friction is 0.5. If the disc starts from rest and is given an angular acceleration 1√2 rad /sec2, the number of revolutions through which the disc turns before the coin slips is
4π
74π
54π
34π
The correct Answer is:B
To solve the problem step by step, we need to analyze the forces acting on the coin and the motion of the disc.
Step 1: Identify the forces acting on the coin
The coin experiences two main forces:
1. The gravitational force (weight) acting downwards: Fg=mg
2. The frictional force acting towards the center of the disc, which provides the necessary centripetal force for circular motion.
Step 2: Write the expression for centripetal force
The centripetal force required to keep the coin moving in a circle of radius r is given by:
Fc=mv2r
Where v is the linear velocity of the coin.
Step 3: Relate linear velocity to angular velocity
The linear velocity v can be expressed in terms of angular velocity ω:
v=ωr
Substituting this into the centripetal force equation gives:
Fc=m(ωr)2r=mω2r
Step 4: Write the expression for frictional force
The maximum frictional force that can act on the coin before it slips is given by:
Ff=μmg
Where μ is the coefficient of friction.
Step 5: Set up the equation for slipping condition
For the coin to remain on the disc, the centripetal force must not exceed the maximum frictional force:
mω2r≤μmg
Dividing both sides by m (assuming m≠0):
ω2r≤μg
Rearranging gives:
ω2≤μgr
Step 6: Calculate the critical angular velocity
Substituting the given values μ=0.5, g=9.8m/s2, and r=1m:
ω2≤0.5×9.81=4.9
Taking the square root:
ω≤√4.9≈2.2136rad/s
Step 7: Relate angular acceleration and angular displacement
The disc starts from rest, so the initial angular velocity ω0=0. The angular displacement θ can be calculated using the equation:
ω2=ω20+2αθ
Substituting ω0=0 and α=1√2:
ω2=2(1√2)θ
Setting ω=2.2136:
(2.2136)2=2(1√2)θ
Calculating (2.2136)2:
4.9=2(1√2)θ
θ=4.9√22=4.9⋅1.41422≈3.465
Step 8: Calculate the number of revolutions
To find the number of revolutions N, we convert the angular displacement from radians to revolutions:
N=θ2π=3.4652π≈3.4656.2832≈0.55
Final Answer
The number of revolutions through which the disc turns before the coin slips is approximately 0.55 revolutions.
---
The coin experiences two main forces:
1. The gravitational force (weight) acting downwards: Fg=mg
2. The frictional force acting towards the center of the disc, which provides the necessary centripetal force for circular motion.
The centripetal force required to keep the coin moving in a circle of radius r is given by:
Fc=mv2r
Where v is the linear velocity of the coin.
The linear velocity v can be expressed in terms of angular velocity ω:
v=ωr
Substituting this into the centripetal force equation gives:
Fc=m(ωr)2r=mω2r
The maximum frictional force that can act on the coin before it slips is given by:
Ff=μmg
Where μ is the coefficient of friction.
For the coin to remain on the disc, the centripetal force must not exceed the maximum frictional force:
mω2r≤μmg
Dividing both sides by m (assuming m≠0):
ω2r≤μg
Rearranging gives:
ω2≤μgr
Substituting the given values μ=0.5, g=9.8m/s2, and r=1m:
ω2≤0.5×9.81=4.9
Taking the square root:
ω≤√4.9≈2.2136rad/s
The disc starts from rest, so the initial angular velocity ω0=0. The angular displacement θ can be calculated using the equation:
ω2=ω20+2αθ
Substituting ω0=0 and α=1√2:
ω2=2(1√2)θ
Setting ω=2.2136:
(2.2136)2=2(1√2)θ
Calculating (2.2136)2:
4.9=2(1√2)θ
θ=4.9√22=4.9⋅1.41422≈3.465
To find the number of revolutions N, we convert the angular displacement from radians to revolutions:
N=θ2π=3.4652π≈3.4656.2832≈0.55
The number of revolutions through which the disc turns before the coin slips is approximately 0.55 revolutions.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )12videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (ROTATIONAL MOTION)60videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)20videos
RACE
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
A small coin is placed on a stationery horizontal disc at a distance r from its centre. The disc starts rotating about a fixed vertical axis through its centre with a constant angular acceleration α. Determine the number of revolutions N, accomplished by the disc before the coin starts slipping on the disc. Find the coefficient of static friction between the coin and the disc is μ9.
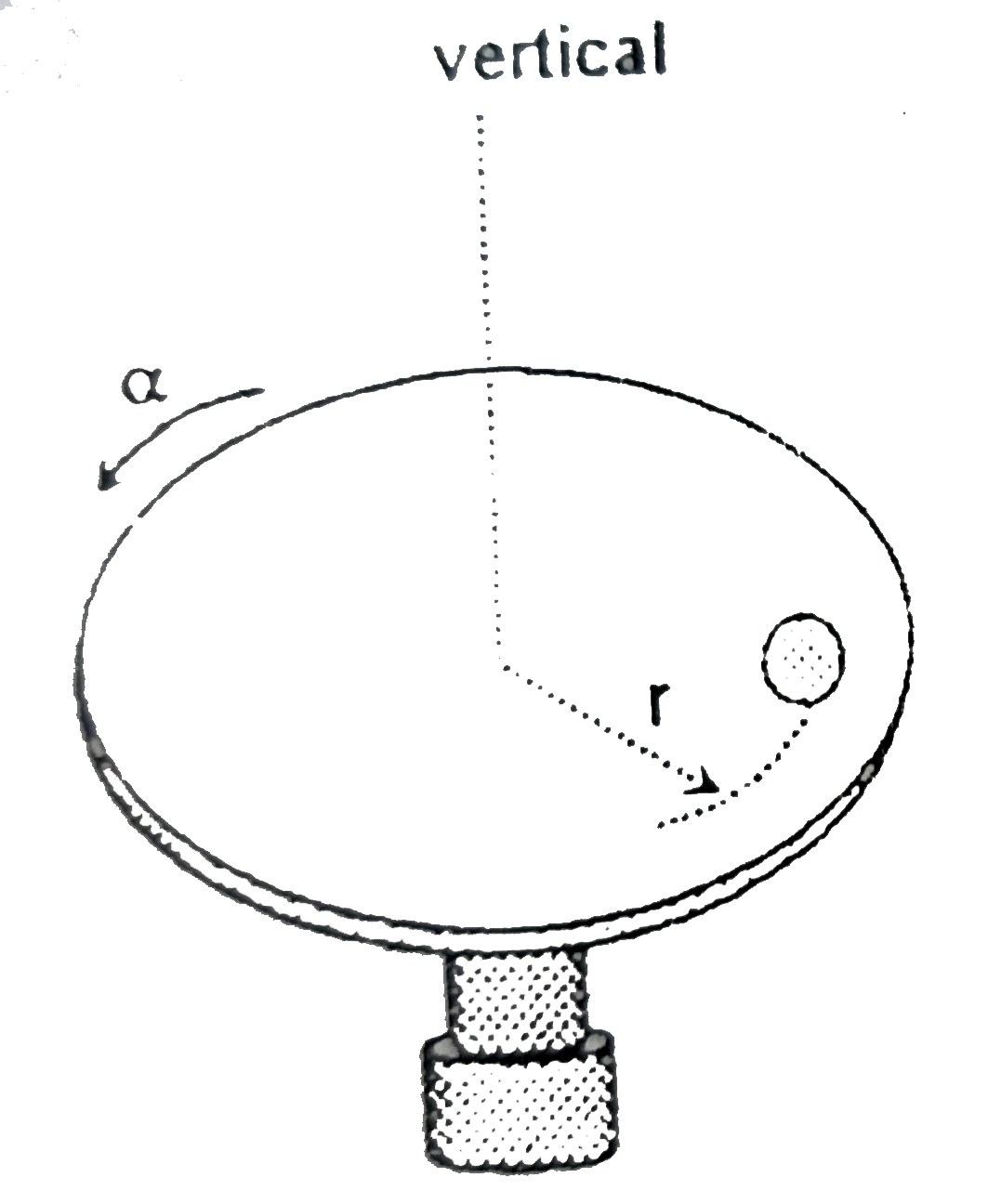 View Solution
View SolutionA small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of hte resultant force on the coin exerted by the disc just before it starts slipping on the disc is :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A disc of radius 0.1 m starts from rest with an angular acceleration of 4.4rad/s2 .Then linear velocity of the point on its after 5 s is
A0.22/sB2.2m/sC4.4m/sD1.1m/s - Question 2 - Select One
A coin of 4 g mass is placed at a distance of 2 cm from the axis of rotation a disc,. If the frequancy of disc is 180 rpm, then the coefficient of friction between the coin at rest and disc will be
A0.07249B7.249C72.49D0.7250 - Question 3 - Select One
A small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is
 A0.2NB0.3NC0.4ND1N
A0.2NB0.3NC0.4ND1N
A coin placed on a horizontal rotating disc, with its centre at 10 cm from the centre of the disc, is about to slip off when the disc performs 60 rpm. Find the coefficient of friction between the coin and the disc.
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
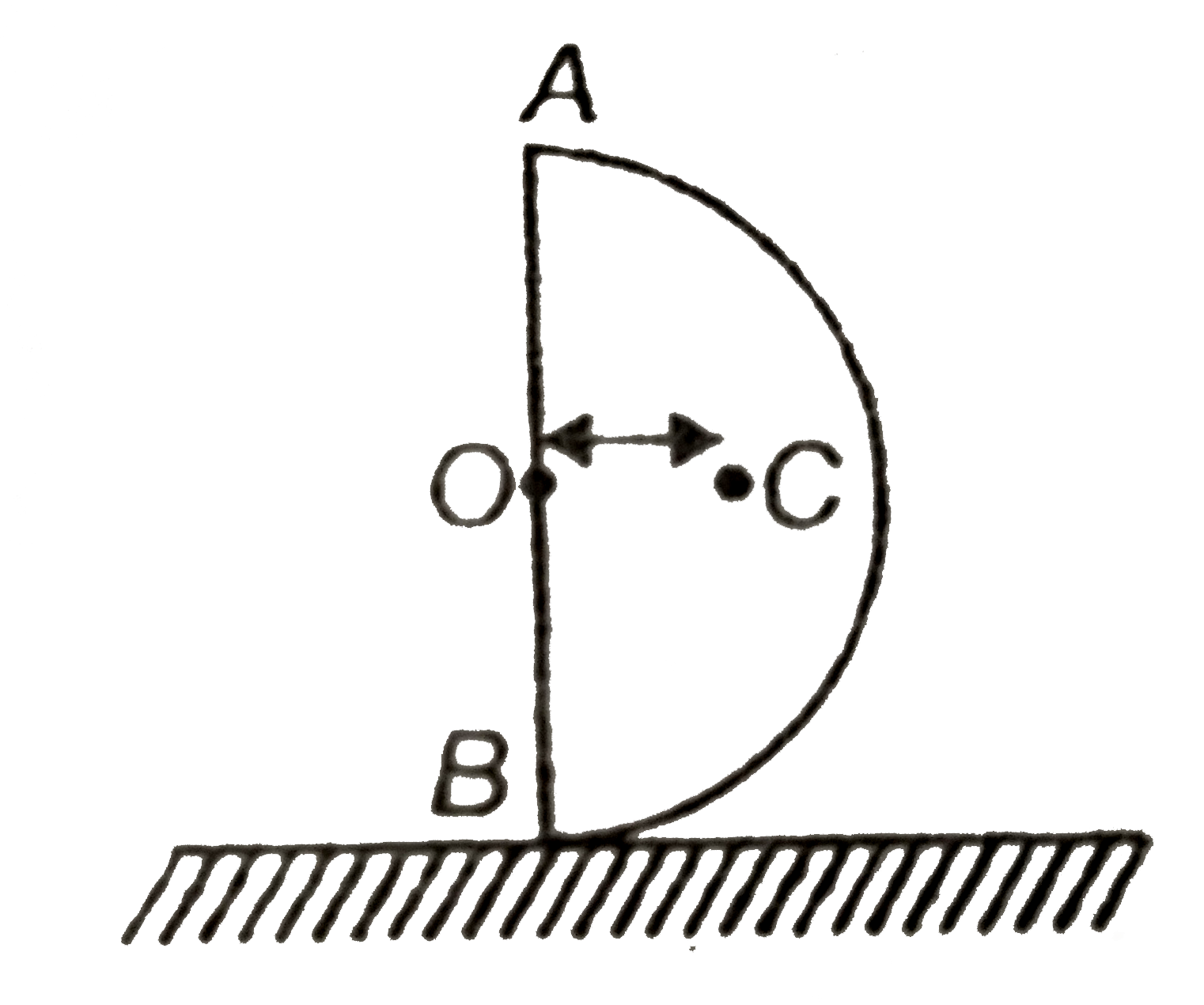
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.View SolutionA coins kept on a horizontal rotating disc has its centre at a distance of 0.25 m from the axis of rotation of the disc .If μis0.2, then the angular velocity of the disc at which the coion will slip off, (g=9.8m/s2)
View SolutionA coin just remains on a disc rotating at a steady rate of 180r.p.m .A coin is kept at a distance of 2 cm from the axis of rotationn . The coefficient of fricition between the coin and the disc is _____ [gg=9.8m/s2]
View SolutionA disc of mass m and radius r placed on a routh horizontal surface. A cue of mass m hits the disc at a height h from the axis passing through centre and parallel to the surface. The disc will start pure rolling for.
View Solution

