Question

A small coin is placed on a stationery horizontal disc at a distance $r$ from its centre. The disc starts rotating about a fixed vertical axis through its centre with a constant angular acceleration $\alpha$. Determine the number of revolutions $N$, accomplished by the disc before the coin starts slipping on the disc. Find the coefficient of static friction between the coin and the disc is ${\mu }_9$.

Explanation

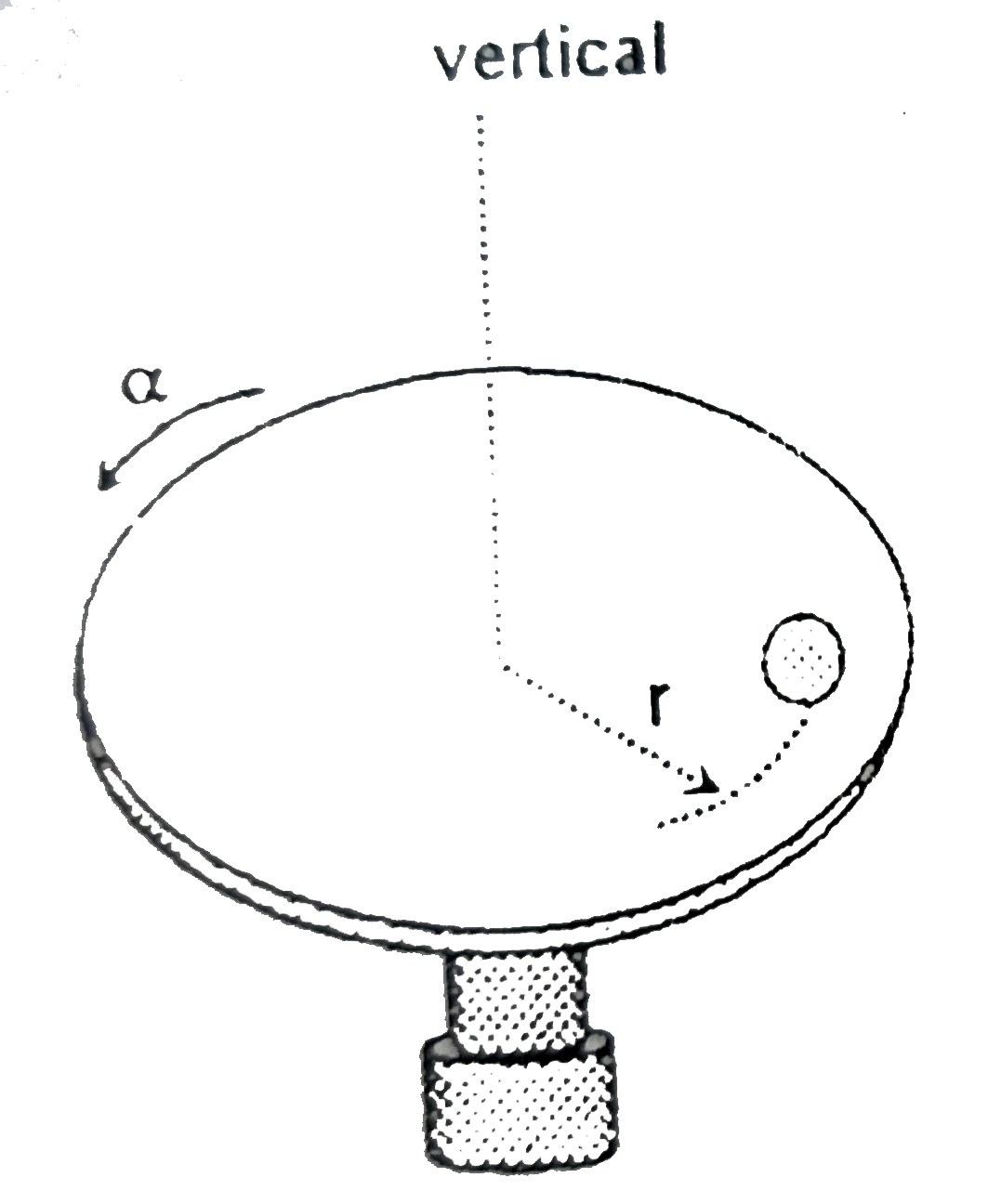
we draw the `FBD` of the coin
`f_(T)=` tangential component of frictional force on coin
`f_(R )=` radial component of frictional force on coin `s`
`f_(T)=malphar`
`f_(r )=momega_(f)^(2)r`
`sqrt(f_(R )^(2)+f_(T)^(2)) le mu_(g)mg`
`2piN=(omega_(f)^(2))/(2alpha)`
Solving the equations, we get
`N=(((mu_(g)g)/(r )-alpha^(2))^(1//2))/(4pialpha)`