A spring is hanging down from the ceiling, and an object of mass m is attached to the free end. The object is pulled down, thereby stretching the spring, and then released. The object oscillates up and down, and the time T required for one complete up-and-down oscillation is given by the equation T=2π√m/k, where k is known as the spring constant. What must be the dimension of k for this equation to be dimensionally correct?
[M][T]
[T][M]
[M][T]2
[T][M]2
The correct Answer is:C
To determine the dimension of the spring constant k in the equation T=2π√mk, we will follow these steps:
Step 1: Identify the dimensions involved
- The time period T has the dimension of time, which is denoted as (T).
- The mass m has the dimension of mass, denoted as (M).
- The spring constant k is what we need to find the dimensions of.
Step 2: Rearrange the equation to isolate k
The equation given is:
T=2π√mk
To isolate k, we can first square both sides:
T2=(2π)2mk
Since (2π)2 is a constant, we can ignore it for dimensional analysis:
T2=mk
Step 3: Rearranging to solve for k
Now, rearranging the equation gives:
k=mT2
Step 4: Determine the dimensions of k
Now we can express the dimensions of k:
- The dimension of mass m is (M).
- The dimension of time squared T2 is (T2).
Thus, the dimension of k can be expressed as:
(k)=(M)(T2)=(M)(T)−2
Step 5: Conclusion
Therefore, the dimension of the spring constant k is:
k=(M)(T)−2
Final Answer
The dimension of k is MT−2.
---
- The time period T has the dimension of time, which is denoted as (T).
- The mass m has the dimension of mass, denoted as (M).
- The spring constant k is what we need to find the dimensions of.
The equation given is:
T=2π√mk
To isolate k, we can first square both sides:
T2=(2π)2mk
Since (2π)2 is a constant, we can ignore it for dimensional analysis:
T2=mk
Now, rearranging the equation gives:
k=mT2
Now we can express the dimensions of k:
- The dimension of mass m is (M).
- The dimension of time squared T2 is (T2).
(k)=(M)(T2)=(M)(T)−2
Therefore, the dimension of the spring constant k is:
k=(M)(T)−2
The dimension of k is MT−2.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)6videos
UNITS AND MEASUREMENT
- BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)11videos
UNITS AND MEASUREMENT
- BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PROBLEM20videos
UNITS AND MEASUREMENT
- BOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PRACTICE QUESTIONS(Integer Type)7videos
THE NUCLEUS
- BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS39videos
VECTORS
Similar Questions
A block of mass 'm' is connected to the lower end of a massless vertically suspended spring. The ball is displaced slightly downward and released, it oscillates up and down. Match the coloum I and column II
 View Solution
View SolutionA massless spring hangs from the ceiling with a small object attached to its lower end. The object is initially held at rest in a position y such that the spring is at its rest length. The object is then released from y and oscillates up and down, with its lowest position being 10cm below y, (a) What is the frequency of the oscillation? (b) What is the speed of the object when it is 8.0 cm below the initial position? (c ) An object of mass 600g is attached to the first object, after which the system oscillates with half the original frequency. What is the mass of the first object? (d) How far below y, is the new equilibrium (rest) position with both objects attached to the spring?
View Solution
Knowledge Check
- Question 1 - Select One
An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2k - Question 2 - Select One
Certain weight is attached with a spring. It is pulled down and then released. It oscillates up and down. Its K.E. will be
Amaximum in the middle of the movementBmaximum at the bottomCmaximum just before it is releasedDconstant - Question 3 - Select One
An ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
A4MgKB2MgKCMgKDMg4K
The end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
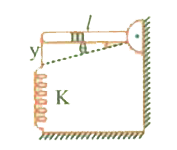 View Solution
View SolutionAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 View Solution
View SolutionA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 View Solution
View SolutionWhen a mass M is attached to the spring of force constant k , then the spring stretches by . If the mass oscillates with amplitude l , what will be maximum potential energy stored in the spring
View Solution

