The term (1/2)ρv2 occurs in Bernoulli's equation, with ρ being the density of a fluid and v its speed. The dimensions of this term are
[M−1L5T2]
[MLT2]
[ML−1T−2]
[M−1L9T−2]
The correct Answer is:C
To find the dimensions of the term (12)ρv2 in Bernoulli's equation, we will break it down step by step.
Step 1: Identify the components of the term
The term we are analyzing is (12)ρv2, where:
- ρ is the density of the fluid.
- v is the speed of the fluid.
Step 2: Write the dimensions of density (ρ)
Density (ρ) is defined as mass per unit volume. The dimensions of mass are (M) and the dimensions of volume are (L3). Therefore, the dimensions of density are:
(ρ)=(M)(L3)=(ML−3)
Step 3: Write the dimensions of speed (v)
Speed (v) is defined as distance traveled per unit time. The dimensions of distance are (L) and the dimensions of time are (T). Therefore, the dimensions of speed are:
(v)=(L)(T)=(LT−1)
Step 4: Calculate the dimensions of v2
To find the dimensions of v2, we square the dimensions of speed:
(v2)=(LT−1)2=(L2T−2)
Step 5: Combine the dimensions of ρ and v2
Now, we can combine the dimensions of ρ and v2 to find the dimensions of the term (12)ρv2:
(ρv2)=(ML−3)⋅(L2T−2)=(ML−3⋅L2T−2)=(ML−1T−2)
Step 6: Conclusion
Thus, the dimensions of the term (12)ρv2 are:
(ML−1T−2)
The term we are analyzing is (12)ρv2, where:
- ρ is the density of the fluid.
- v is the speed of the fluid.
Density (ρ) is defined as mass per unit volume. The dimensions of mass are (M) and the dimensions of volume are (L3). Therefore, the dimensions of density are:
(ρ)=(M)(L3)=(ML−3)
Speed (v) is defined as distance traveled per unit time. The dimensions of distance are (L) and the dimensions of time are (T). Therefore, the dimensions of speed are:
(v)=(L)(T)=(LT−1)
To find the dimensions of v2, we square the dimensions of speed:
(v2)=(LT−1)2=(L2T−2)
Now, we can combine the dimensions of ρ and v2 to find the dimensions of the term (12)ρv2:
(ρv2)=(ML−3)⋅(L2T−2)=(ML−3⋅L2T−2)=(ML−1T−2)
Thus, the dimensions of the term (12)ρv2 are:
(ML−1T−2)
Topper's Solved these Questions
- UNITS AND MEASUREMENT BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- UNITS AND MEASUREMENT BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
11 Videos
- UNITS AND MEASUREMENT BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PROBLEM
20 Videos
- THE NUCLEUSBOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PRACTICE QUESTIONS(Integer Type)
7 Videos
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS
39 Videos
Similar Questions
Define the term density. Give its units and dimensions.
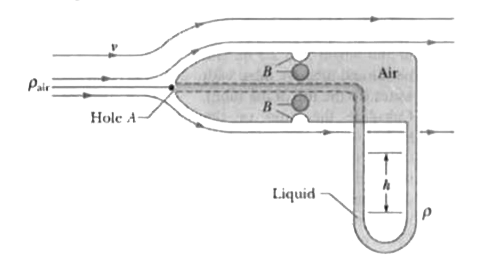
View SolutionA pitot tube Fig. is used to determine the air speed of an airplane. It consists of an outer tube with a number of small holes B (four are shown that allow air into the tube, that tube is connected to one arm of a U-tube. The other arm of the U-tube is connected to hole A at the front end of the device, which points in the direction the plane is headed. At A the air becomes stagnant so that vA = 0. At B, however, the speed of the air presumably equals the airspeed v of the plane. (a) Use Bernoulli's equation to show that
v=√2ρghρair
where ρ is the density of the liquid in the U-tube and his the difference in the liquid levels in that tube. (b) Suppose that the tube contains alcohol and the level difference h is 20.0 cm. What is the plane's speed relative to the air? The density of the air is 1.03kg/m3 and that of alcohol is 810 kg/m3
View Solution
Knowledge Check
If P is the pressure of a gas and ρ is its density , then find the dimension of velocity in terms of P and ρ .
AP1/2ρ−1/2BP1/2ρ1/2CP−1/2ρ−1/2DP−1/2ρ−1/2The 2nd term of an AP is 13 and its 5th term is 25. What is its 17th term?
A69B73C77D81_E01_053_Q01.png)
There are three different liquids, with densities ρ1,ρ2 and ρ3 in a U-shaped container as shown in the picture the lengths shown are H1=15cm and H2=10cm which of the following equations gives the correct relation between the densities of the fluids in the container?A3ρ3=2ρ1+ρ2Bρ3=2ρ1+3ρ2C2ρ3=3ρ1+ρ2Dρ3=3ρ1+2ρ2
If the fifth term of a G.P. is 2, then write the product of its 9 terms.
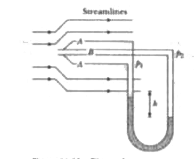
View SolutionFigure shows a device called Pitot tube . It measures the velocity of moving fluids . Determine the velocity of the fluid in terms of the density ρ the density of the fluid in manometer (U-tube) σ and the height h .
View SolutionDefine the term speed. Is it a scalar or vector quantity ? Give its unis and dimensions.
View SolutionA venturi meter is used to measure the flow speed of a fluid in a pipe . The meter is connected between two sections of the pipe (Fig) the cross-sectional area A of the entrance and exit of the meter matches the pipe's cross-sectional area a with speed v . A manometer connects the wider portion of the meter to the narrower portion . The change in the fluid's speed is accompanied by a change Δp in the fluid 's pressure , which causes a height difference h of the liquid in the two arms of the manometer. (Here , Δp means pressure in the throat minus pressure in the pipe).
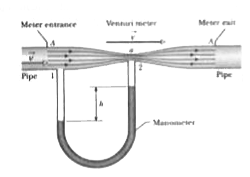
(a) By applying Bernoulli's equation and the equation of continuity to points 1 and 2 in Fig show that
V=√2a2Δpρ(a2−A2)
where r is the density of the fluid .
View SolutionIf an additional pressure Δp of a saturated vapour over a convex spherical surface of a liquid is considerably less than the vapour pressure over a plane surface, then Δp=(ρv/ρl)2α/r, where ρv and ρl) are the densities of the vapour and the liquid, α is the surface tension, and r is the radius of curvature of the surface. Using this formula, find the diameter of water droplets at which the saturated vapour pressure exceeds the vapour pressure over the plane surface by η=1.0% at a temperature t=27∘C. The vapour is assumed to be an ideal gas.
View Solution
