The mass at C is attached to the vertical pole AB by two wires. The assembly is rotating about AB at the constant angular speed ω. If the force in wire BC is twice the force in AC, determine the value of ω, see fig.
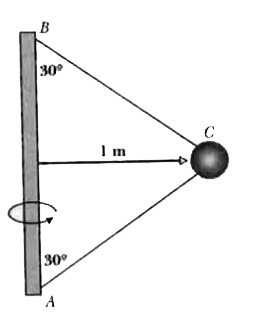
The correct Answer is:(g√3)1/2
Step by step video & image solution for The mass at C is attached to the vertical pole AB by two wires. The assembly is rotating about AB at the constant angular speed omega. If the force in wire BC is twice the force in AC, determine the value of omega, see fig. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(SINGLE CORRECT CHOICE TYPE)
40 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
ABC is a triangular frame made of a conducting wire and is right angled at B. Its side BC is vertical and AB is horizontal. The frame is placed in a uniform magnetic field B in vertically upward direction. The frame is rotated about its side BC with constant angular speed ω. Resistance of the entire frame is R. Neglect gravity. Length AB=L,BC=2L.
(a) Find the torque needed to keep the frame rotating with constant angular speed.
(b) Find the potential difference between points A and C.
View SolutionA copper rod AB of length l is rotated about one end A with a constant angular velocity ω. Calculate the electric field at a distance x from the axis of rotation. Also determine PD between A and B.
View Solution
Knowledge Check
In the given figure, a smooth parabolic wire track lies in the xy-plane (vertical). The shape of track is defined by the equation y=x2. A ring of mass m which can slide freely on the wire track, is placed at the position A(1,1). The track is rotated with constant angular speed ω such that there is no relative slipping between the ring and the track. The value of ω is
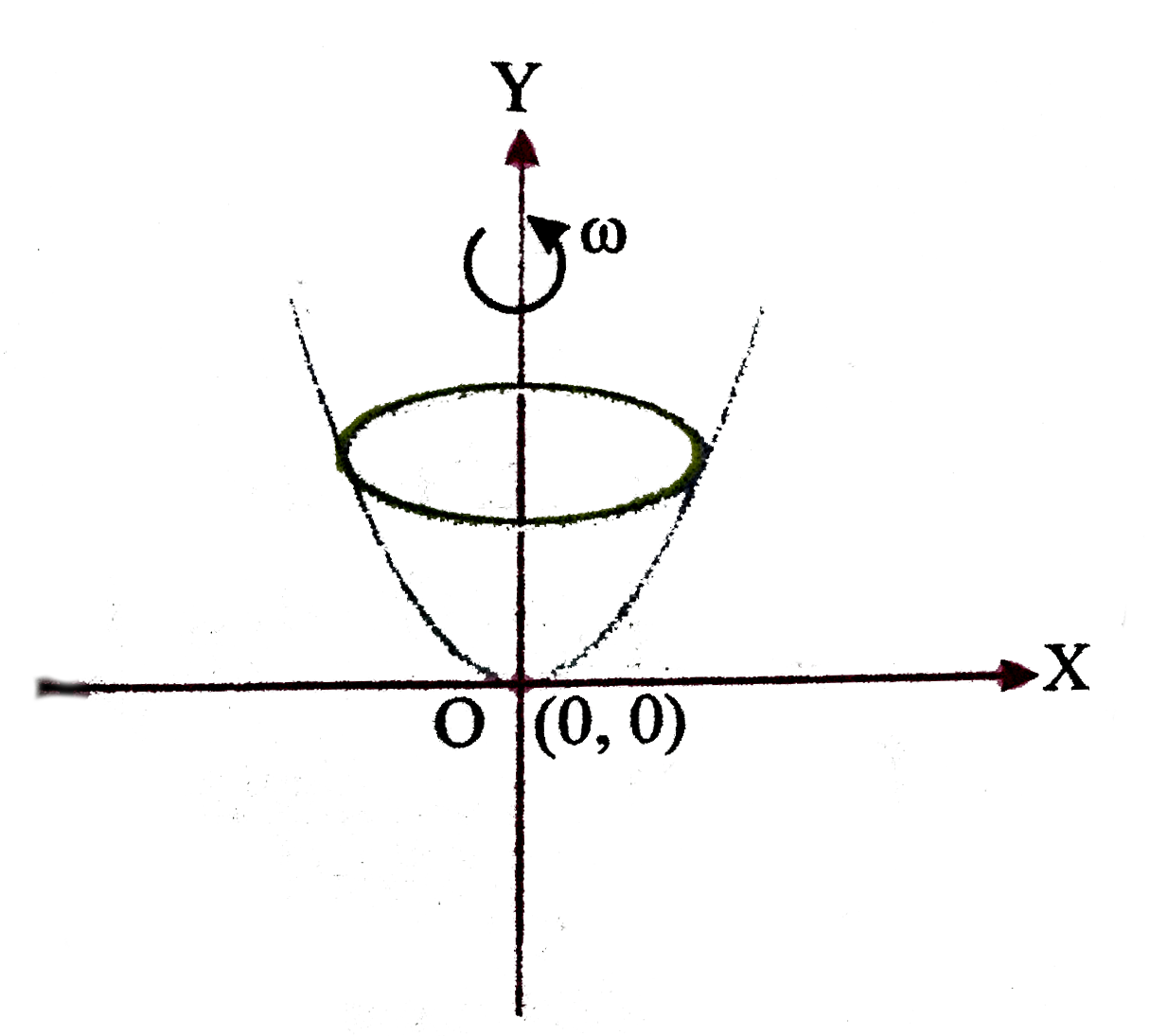 A√g/2B√gC√2gD2√g
A√g/2B√gC√2gD2√gA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
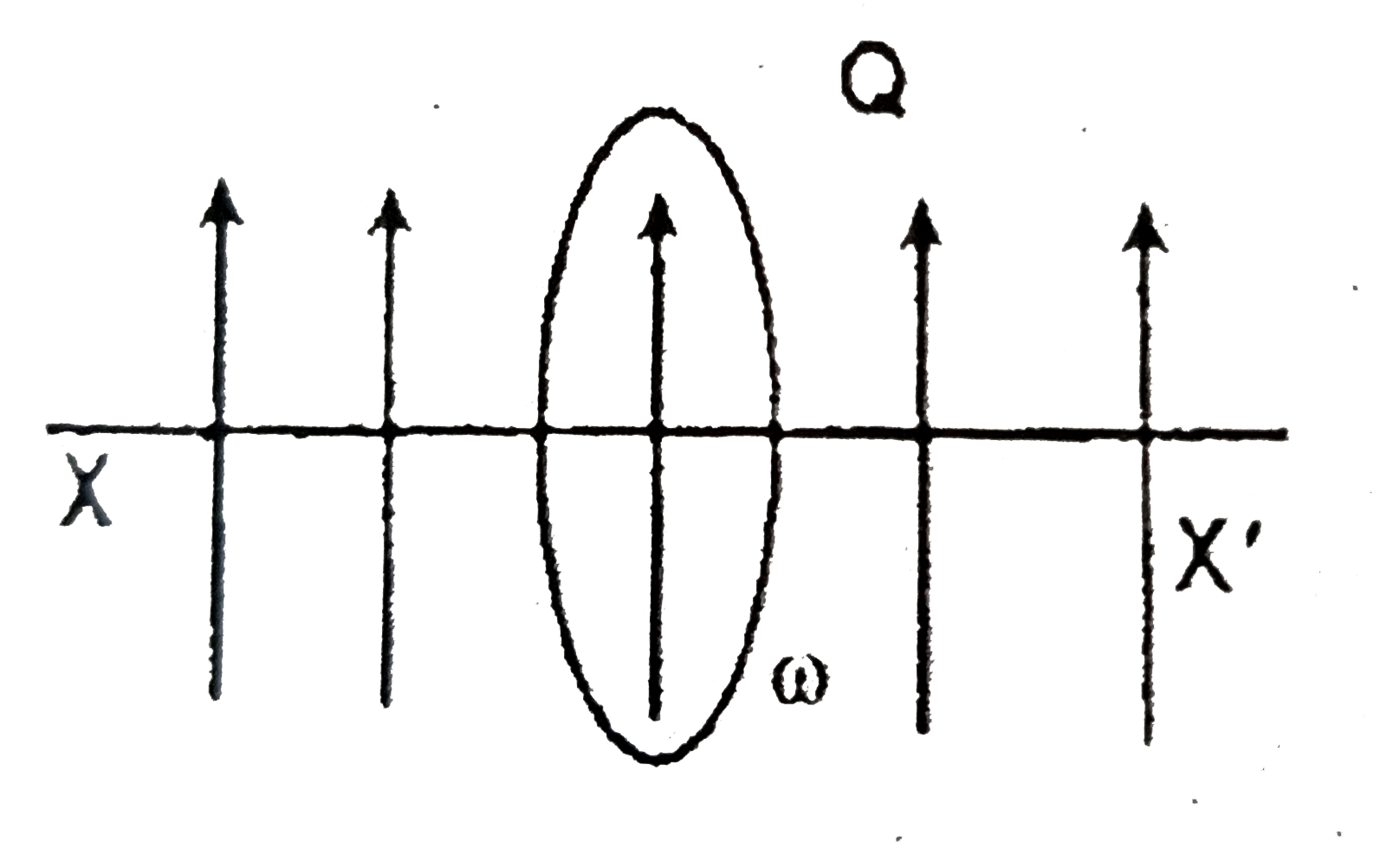 AzeroBωRB/πC2QωBRDnone of these
AzeroBωRB/πC2QωBRDnone of theseA small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then is equal to:
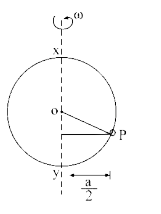 A2gaBg2aC2ga√3Dg√32a
A2gaBg2aC2ga√3Dg√32a
A package of mass m is placed inside a drum that rotates in the vertical plane at the constant angular speed ω=1.36 rad/s. If the package reaches the position θ=45∘ before slipping determine the coefficient of friction between the package and drum. See fig.
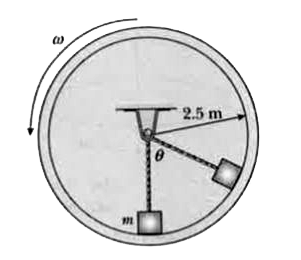
View SolutionA small wedge whose base is horizontal is fixed to a vertical rod as shown in fig . The sloping side of the weidgeis frictionless and the wedge is span with a constant angular speed ω about vertical axis as shown in the fig find the
a. value of angular speed ω for which the block of mass m just does not slide down the wedge.
b. normal reaction on the block by wedge when block does not slip relative to wedge.

View SolutionA copper wire of negligible mass, length l and corss-section A is kept on a smooth horizontal tabel with one end fiexed. A ball of mass m is attached to the other end. The wire and the ball are rotating with an angular velocity ω. If elongation in the wire is Δl, obtain the expression for the Young's modulus.
View SolutionA closed chain A of mass m = 0.36kg is attached to a vertical rotating shaft by means of thread showin in fig. and rotated with a constant angular velocity ω=35rad/s. The thread forms an angle θ=45∘ with the vertical. Then the tension of the thread is
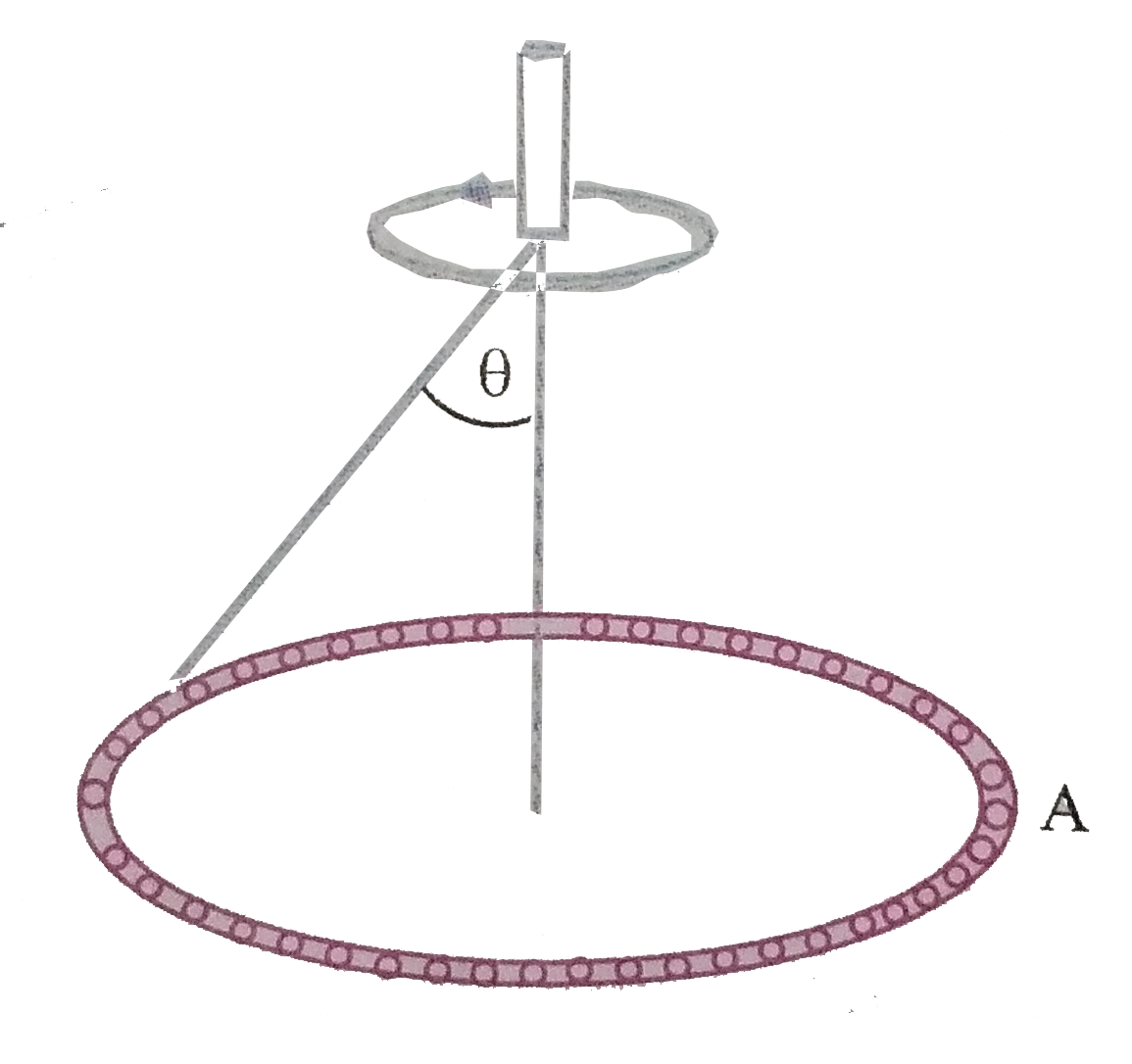
View SolutionA steel wire of negligible mass length L0 and cross sectional area A0 is kept on a smooth horizontal table with one end fixed. A ball of mass M is attached to the other end. The wire and ball are rotating with angular velocity ω . If elongation in the wire is ΔL, then the value of Young's modulus of elasticity will be
View Solution
