A small 0.25 kg collar C many slide on a semicircular rod which is made to rotate about the vertical axis yy' at a constant of 7.5 rad/s. Determine the value of θ for which the collar will not slide on the rod, assuming no friction between the collar and the rod.
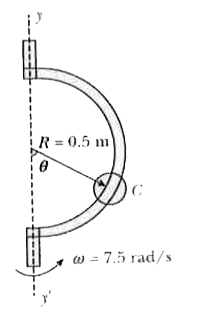
The correct Answer is:cos−1(925)
Step by step video & image solution for A small 0.25 kg collar C many slide on a semicircular rod which is made to rotate about the vertical axis yy' at a constant of 7.5 rad/s. Determine the value of theta for which the collar will not slide on the rod, assuming no friction between the collar and the rod. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(SINGLE CORRECT CHOICE TYPE)
40 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
A small collar of mass m = 100 g slides over the surface of a horizontal circular rod of radius R = 0.3 m. The coefficient of friction between the rod and the collar is μ=0.8. Find the angle made with vertical by the force applied by the rod on the collar when speed of the collar is V = 2 m/s.
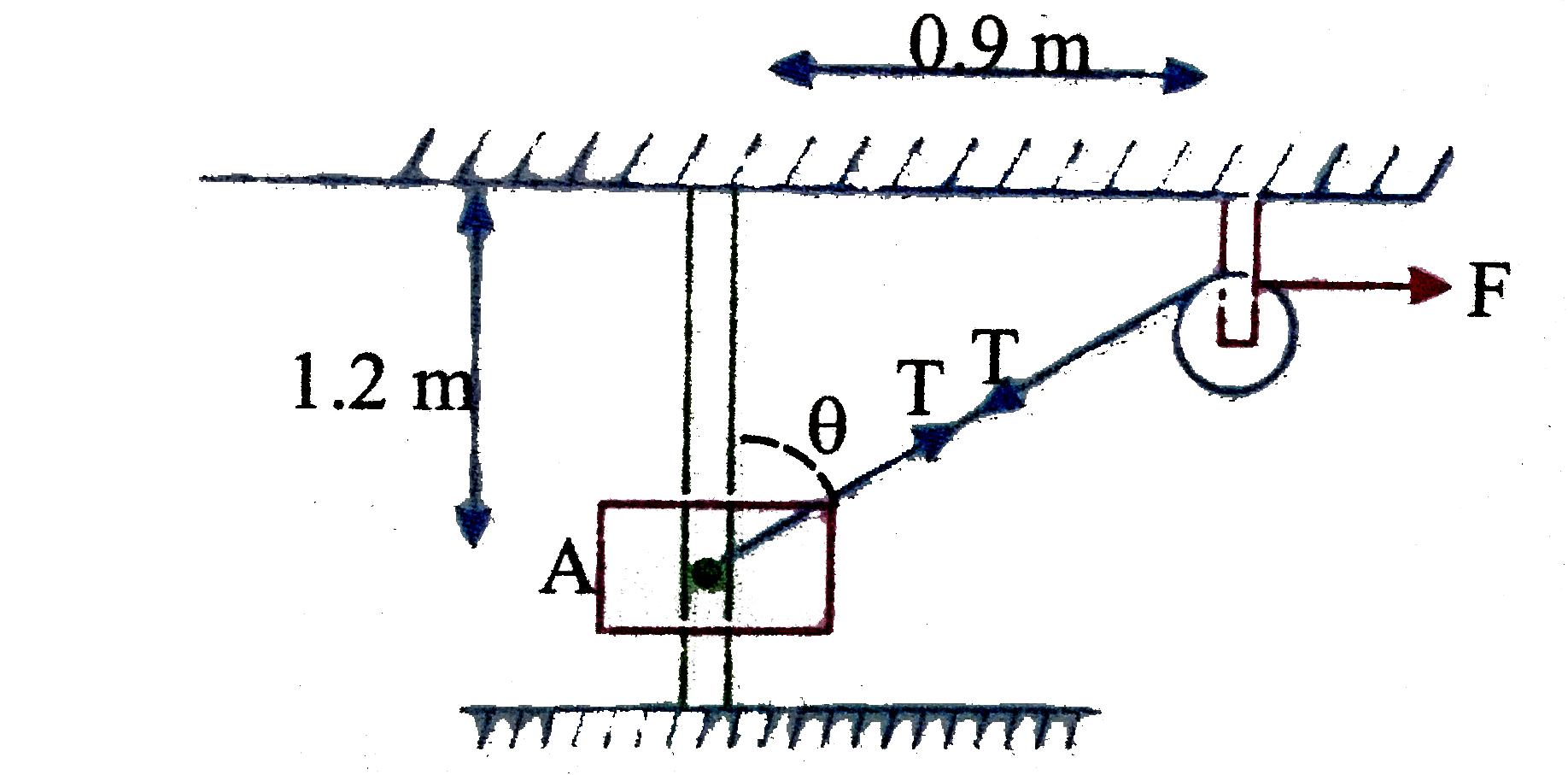
View SolutionThe 50N collar starts from rest at A and is lifted with a constant speed of 0.6m/s along the smooth rod. Determine the power developed by the force F at the instant shown.
.
View Solution
Knowledge Check
Find the minimum value of F for which 5 kg being to slide if the coefficient of friction between the blocks is changed to 0.5 :A10 NB30 NC45 NDno value existThe 50N collar starts from rest at A and is lifted with a constant speed of 0.6m/s along the smooth rod. Determine the power developed by the force F at the instant shown.
.A20WB30WC10WD40WAB is a light rigid rod. Which is rotating about a vertical axis passing through A,A spring of force constant K and natural length l is attached at A and its other end is attached to a small bead of mass m. The bead can slide without friction on the rod. At the initial moment the bead is at rest (w.rt. the rod) and the spring is unstreached Select correct option
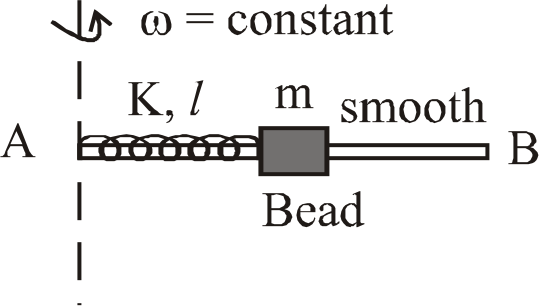AThe maximum velocity attained by the bead w.r.t the rod is given by Vmax=√mω4l2K−mω2BThe maximum velocity attained by the bead w.r.t the rod is given by Vmax=√(mω4+Kmω2−K)ω2l2CThe maximum extension in the spring is given by Xmax=2mω2lK−mω2DThe maximum value of contact force between the bead and the rod is greater than mg
The 50N collar starts from rest at A and is lifted with a constant speed of 0.6m/s along the smooth rod. Determine the power developed by the force F at the instant shown.
.
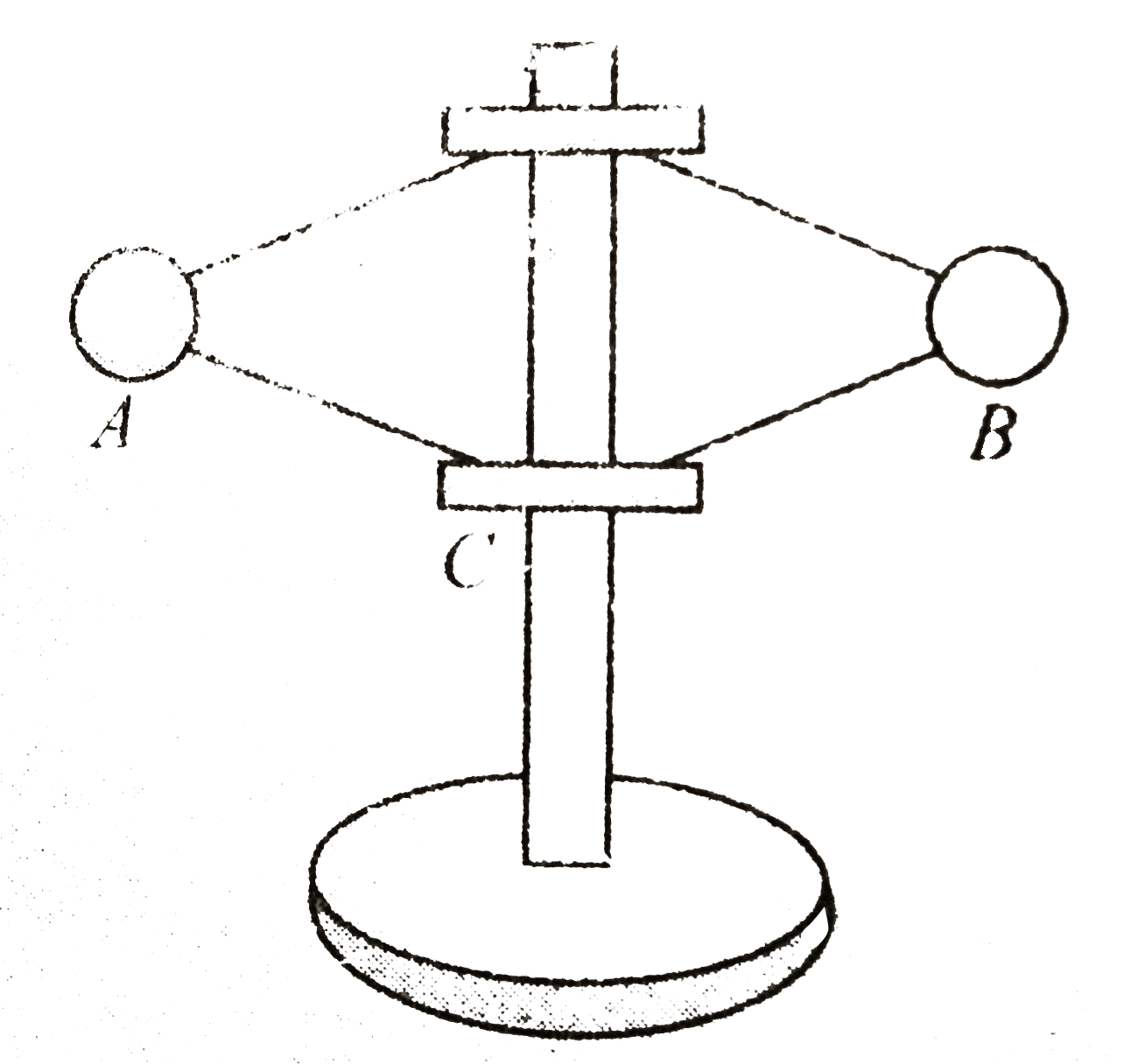
View SolutionThe steel balls A and B have a mass of 500g each and al rotating about the vertical axis with an angular velocity of 4rad/s at a distance of 15CM from the axis. Collar C is now forced down until the balls are at a distance 5CM from the axis. How Much work must be done move the collar down?
View SolutionA uniform rod of mass M and length L is hinged at its lower end so as to rotate freely in the vertical plane of the fig. There is a small tight fitting the hinged end. A small mass less pin welded to the rod supports the bead. The system is released from the vertical position shown. It was observed that the bead just begins to slide on the rod when the rod becomes horizontal.
(a) Find the normal contact force between the rod and the bead when the rod gets horizontal. What is the direction of this force?
(b) Find the coefficient of friction between the bead and rod.
View SolutionAB is a light rigid rod. Which is rotating about a vertical axis passing through A,A spring of force constant K and natural length l is attached at A and its other end is attached to a small bead of mass m. The bead can slide without friction on the rod. At the initial moment the bead is at rest (w.rt. the rod) and the spring is unstreached Select correct option
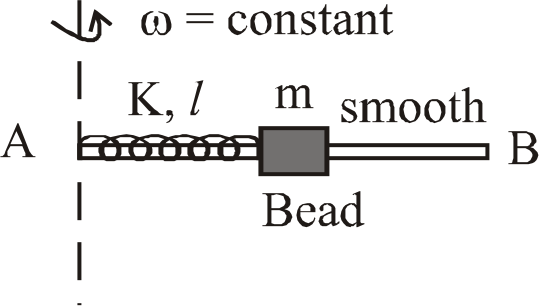
View SolutionThe 0.8 kg collar slides freely on the fixed vertical circular rod. Calculate the velocity v of the collar as it hits the stop at B if it elevated from rest at A by the actionof the constant 40N force in the cord. The cord is guided by the small fixed pulleys.
View Solution