A space vehicle is traveling at 4800 km/h relative to Earth when the exhausted rocket motor (mass 4m) is disengaged and sent backward. The relative speed between motor and command module (mass m) is then 82 km/h. What is the speed of the command module relative to Earth just after the separation ?
The correct Answer is:4.9×103 km/h
To solve the problem, we will use the principle of conservation of momentum and the information provided about the velocities involved.
1. Identify the masses and initial velocity:
- Mass of the command module (CM) = m
- Mass of the rocket motor (RM) = 4m
- Total mass of the space vehicle = m+4m=5m
- Initial speed of the space vehicle relative to Earth, Vs=4800 km/h.
2. Define the velocities after separation:
- Let the speed of the command module after separation be VCM.
- The rocket motor is sent backward with a relative speed of 82 km/h with respect to the command module. Therefore, the speed of the rocket motor after separation can be expressed as:
VR=VCM−82 km/h
3. Apply conservation of momentum:
- Before separation, the total momentum of the system is:
Pinitial=(5m)⋅Vs=5m⋅4800
- After separation, the total momentum is:
Pfinal=(m⋅VCM)+(4m⋅VR)
- Substituting VR:
Pfinal=m⋅VCM+4m⋅(VCM−82)
- Simplifying this gives:
Pfinal=m⋅VCM+4m⋅VCM−328m=5m⋅VCM−328m
4. Set initial momentum equal to final momentum:
5m⋅4800=5m⋅VCM−328m
- Dividing through by m (assuming m≠0):
5⋅4800=5⋅VCM−328
5. Solve for VCM:
24000+328=5⋅VCM
5⋅VCM=24328
VCM=243285=4865.6 km/h
Conclusion:
The speed of the command module relative to Earth just after the separation is approximately 4865.6 km/h.
- Mass of the command module (CM) = m
- Mass of the rocket motor (RM) = 4m
- Total mass of the space vehicle = m+4m=5m
- Initial speed of the space vehicle relative to Earth, Vs=4800 km/h.
- Let the speed of the command module after separation be VCM.
- The rocket motor is sent backward with a relative speed of 82 km/h with respect to the command module. Therefore, the speed of the rocket motor after separation can be expressed as:
VR=VCM−82 km/h
- Before separation, the total momentum of the system is:
Pinitial=(5m)⋅Vs=5m⋅4800
- After separation, the total momentum is:
Pfinal=(m⋅VCM)+(4m⋅VR)
- Substituting VR:
Pfinal=m⋅VCM+4m⋅(VCM−82)
- Simplifying this gives:
Pfinal=m⋅VCM+4m⋅VCM−328m=5m⋅VCM−328m
5m⋅4800=5m⋅VCM−328m
- Dividing through by m (assuming m≠0):
5⋅4800=5⋅VCM−328
24000+328=5⋅VCM
5⋅VCM=24328
VCM=243285=4865.6 km/h
The speed of the command module relative to Earth just after the separation is approximately 4865.6 km/h.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
Two points mass m and 2m are kept at a distance a. Find the speed of particles and their relative velocity of approach when separation becomes a/2.
View SolutionA space shuttle while travelling at a speed of 4000 km/h with respect to the earth disconnects and ejects a module backward, weighing one sixth of the resudual part. If the shuttle ejects the disconnected module at a speed of 100 km/h with respect to the state of the shuttle before the ejection, find the final velocity of the shuttle.
View Solution
Knowledge Check
- Question 1 - Select One
A car of mass 400 kg and travelling at 72 km/h hits a truck of mass 4000 kg and travelling at 9 km/hr in the same direction. The car bounces bact at a speed of 18 km/h. What is the speed of the truck after the impact?
A9km/hB18km/hC27km/hD36km/h - Question 2 - Select One
A passenger is walking on an escalator at a speed of 6 km/h relative to the escalator. The escalator is moving at 3 km/h relative to ground and has a total length of 120 m. The time taken by him to reach the end of the escalator is
A16 sB48 sC32 sD80 s
A space shuttle of mass M, moving at 4000 kph relative to earth ejects a capsule backward of mass M/5. if speed of ejection of capsule is 120 kph relative to state of shuttle before ejection, find the final velocity of the shuttle.
View SolutionA plane is travelling eastward at a speed of 500kmh−1. But a 90kmh−1 wind is blowing southward. What is the direction and speed of the plane relative to the ground ?
View SolutionA projectile is to be launched from the surface of the earth so as to escape the solar system. Consider the gravitational force on the projectile due to the earth and the sun nly. The projectile is projected perpendicular to the radius vector of the earth relative to the centre of the sun in the direction of motion of the earth. Find the minimum speed of projection relative to the earth so that the projectile escapes out of the solar system. Neglect rotation of the earth. mass if the sum Ms2×1030kg, Mass of the earth Me=6.4×1024kg Radius if the earthRe=6.4×106m, Earth- Sun distence r=1.5×1011m
View SolutionA cube of mass m and height H slides with a speed v. It strikes the obstacle of height h=(H4). Find the speed of the CM of the cube just after the collision.
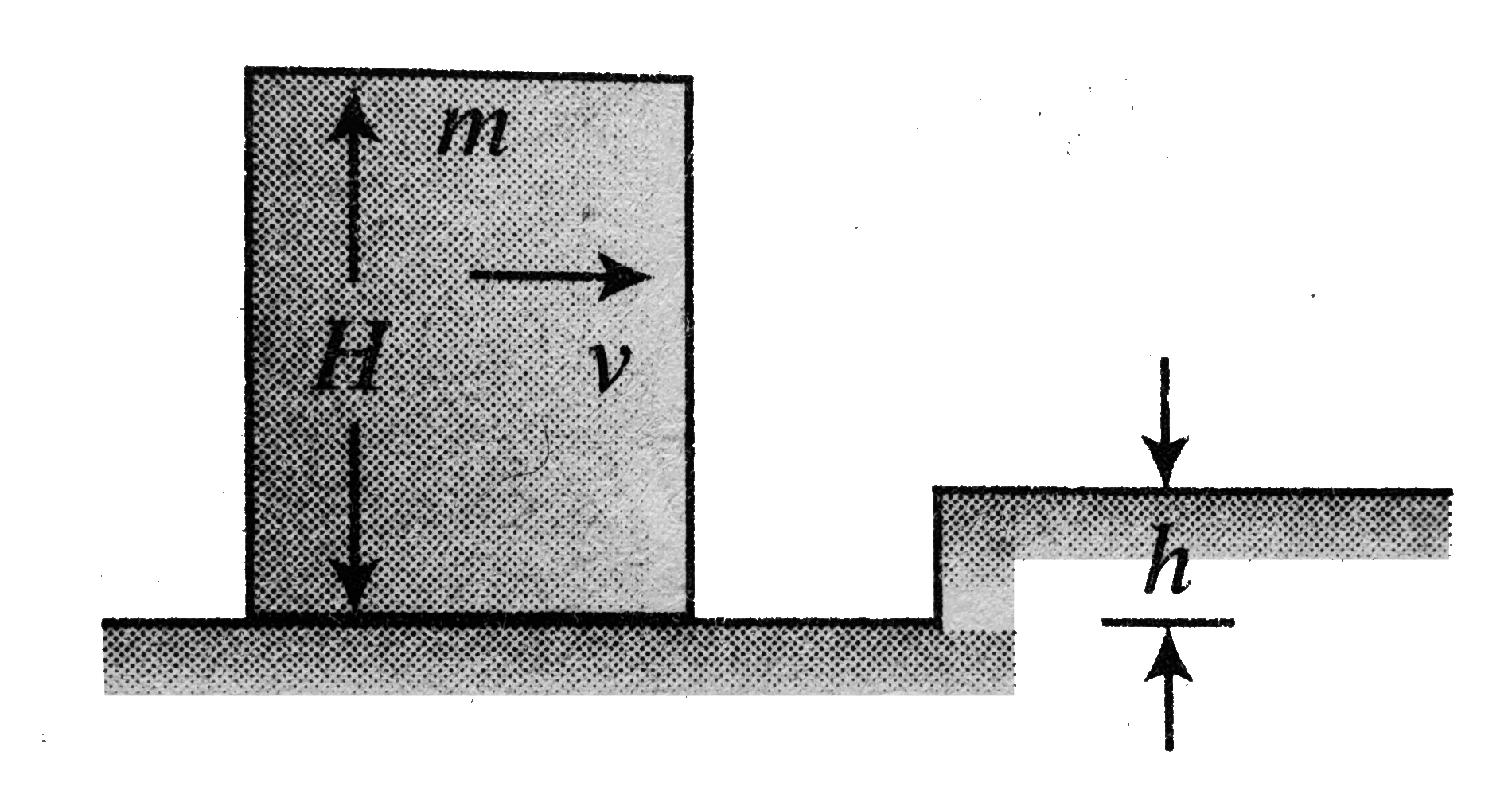 View Solution
View SolutionConsider a rocket that is in deep space and at rest relative to an inertial reference frame. The rocket's engine is to be fired for a certain interval. What must be the rocket's mass ratio (ratio of initial to final mass) over that interval if the rocket's original speed relative to the inertial frame is to be equal to (a) the exhaust speed (speed of the exhaust products relative to the rocket) and (b) 2.0 times the exhaust speed?
View SolutionAfter flying for 18 min in a wind blowing 42 km/h at an angle of 20∘ south of east, an airplane pilot is over a town that is 55 km due north of the starting point. What is the speed of the airplane relative to the air?
View Solution

