A 2.5-kg ball and a 5.0-kg ball have an elastic collision. Before the collision, the 2.5-kg ball was at rest and the other ball had a speed of 3.5 m/s. What is the kinetic energy of the 2.5-kg ball after the collision?
1.7 J
3.4 J
8.1 J
27 J
The correct Answer is:D
To solve the problem of the elastic collision between a 2.5-kg ball and a 5.0-kg ball, we will follow these steps:
Step 1: Understand the Problem
We have two balls:
- Ball 1 (m1 = 2.5 kg) is at rest (u1 = 0 m/s).
- Ball 2 (m2 = 5.0 kg) is moving with a speed of 3.5 m/s (u2 = 3.5 m/s).
We need to find the kinetic energy of Ball 1 after the collision.
Step 2: Use Conservation of Momentum
In an elastic collision, the total momentum before the collision is equal to the total momentum after the collision.
The momentum before the collision:
pinitial=m1⋅u1+m2⋅u2=2.5⋅0+5.0⋅3.5=17.5kg m/s
Let v1 be the final velocity of Ball 1 and v2 be the final velocity of Ball 2 after the collision. The momentum after the collision is:
pfinal=m1⋅v1+m2⋅v2
Setting the initial and final momentum equal:
17.5=2.5⋅v1+5.0⋅v2(1)
Step 3: Use Conservation of Kinetic Energy
In an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
The kinetic energy before the collision:
KEinitial=12m1u21+12m2u22=12⋅2.5⋅02+12⋅5.0⋅(3.5)2
=0+12⋅5.0⋅12.25=30.625J
The kinetic energy after the collision:
KEfinal=12m1v21+12m2v22(2)
Setting the initial and final kinetic energy equal:
30.625=12⋅2.5⋅v21+12⋅5.0⋅v22(3)
Step 4: Solve the Equations
From equation (1):
5.0⋅v2=17.5−2.5⋅v1
v2=17.5−2.5⋅v15.0(4)
Substituting equation (4) into equation (3):
30.625=12⋅2.5⋅v21+12⋅5.0⋅(17.5−2.5⋅v15.0)2
This will lead to a quadratic equation in terms of v1. After solving the quadratic equation, we can find the value of v1.
Step 5: Calculate Kinetic Energy of Ball 1
Once we find v1, we can calculate the kinetic energy of the 2.5-kg ball after the collision using:
KEfinal=12m1v21
We have two balls:
- Ball 1 (m1 = 2.5 kg) is at rest (u1 = 0 m/s).
- Ball 2 (m2 = 5.0 kg) is moving with a speed of 3.5 m/s (u2 = 3.5 m/s).
In an elastic collision, the total momentum before the collision is equal to the total momentum after the collision.
pinitial=m1⋅u1+m2⋅u2=2.5⋅0+5.0⋅3.5=17.5kg m/s
pfinal=m1⋅v1+m2⋅v2
17.5=2.5⋅v1+5.0⋅v2(1)
In an elastic collision, the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
KEinitial=12m1u21+12m2u22=12⋅2.5⋅02+12⋅5.0⋅(3.5)2
=0+12⋅5.0⋅12.25=30.625J
KEfinal=12m1v21+12m2v22(2)
30.625=12⋅2.5⋅v21+12⋅5.0⋅v22(3)
From equation (1):
5.0⋅v2=17.5−2.5⋅v1
v2=17.5−2.5⋅v15.0(4)
30.625=12⋅2.5⋅v21+12⋅5.0⋅(17.5−2.5⋅v15.0)2
Once we find v1, we can calculate the kinetic energy of the 2.5-kg ball after the collision using:
KEfinal=12m1v21
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Linked Comprehension)6videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Problems46videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
In the game of billiards, all the balls have approximately the same mass, about 0.17 kg. In the figure, the cue ball strikes another ball such that it follows the path shown. The other ball has a speed of 1.5 m/s immediately after the collision. What is the speed of the cue ball after the collision?
 View Solution
View SolutionA ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mas 1.0 kg. After the collision the balls stick together ane remain motionless. What was the velocity of the 1.0 kg block before the collision?
View Solution
Knowledge Check
- Question 1 - Select One
Two smooth balls A and B, each of mass m and radius R, have their centres as shown in fig. Ball A, moving along positive x-axis, collides with ball B. Just before the collision, speed of ball 'A' is 4m/s and ball 'B' is stantionary. The collision

Velocity of the ball 'A' just after the collision isA(i+√3ˆj)m/sB(i−√3ˆj)m/sC(2i+√3ˆj)m/sD(2i+2ˆj)m/s - Question 2 - Select One
Suppose a golf ball is hurled at a heavy bowling ball initially at rest and bounces elastically from the bowling ball after the collision
Athe golf ball has the greater momentium and the greater kinetic energyBthe bowling ball has the greater momentium and the greater kinetic energyCthe golf ball has the greater momentium but has the smaller kinetic energyDthe bowling ball has the greater momentium but has the smaller kinetic energy - Question 3 - Select One
A ball moving with velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at an angle of 30∘ with the original line of motion. What are the speeds of the balls after the collision ?
A√32msecB3msecC2√3msecD√3msec
A 5 kg ball and a 10 ball approach each other with equal speeds of 21ms−1 . Determine their speeds after the elastic collision.
View SolutionTwo smooth balls A and B, each of mass m and radius R, have their centres as shown in fig. Ball A, moving along positive x-axis, collides with ball B. Just before the collision, speed of ball 'A' is 4m/s and ball 'B' is stantionary. The collision
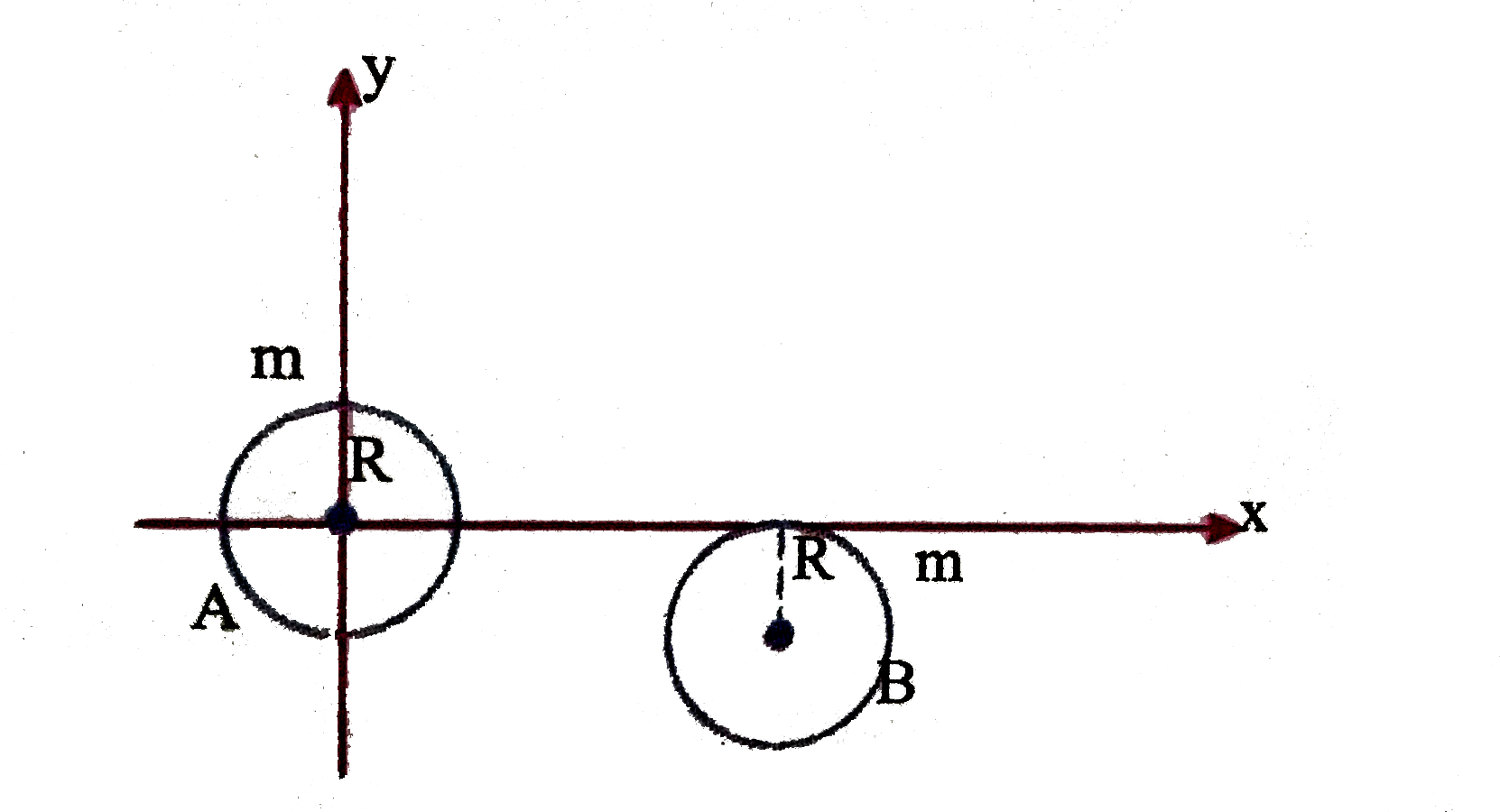
Coefficient of restitution during the collision is changed to 12, keeping all other parameters unchanged. What is the velocity of the ball 'B' after the collision.View SolutionA ball moving with a speed of 10 m s−1 strikes an identical ball such that after the collision the direction of each ball makes an angle 45∘ with the original line of motion. Find the speeds of the two balls after the collision.
View SolutionTwo smooth balls A and B, each of mass m and radius R, have their centre at (0,0,R) and (5R,-R,R) respectively, in a coordinate system as shown. Ball A, moving along positive x-axis, collides with ball B. Just before the collision, speed of ball A is 4m/s and ball B is stationary. The collision between the balls is elastic. Velocity of the ball A just after the collsion is
 View Solution
View SolutionTwo massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png) View Solution
View Solution

