Figure 15.16a shows a thin rod whose length L is 12.4cm and whose mass m is 135g, suspended at its midpoint from a larg wire. Its period $T_{a}$ of angular SHM is measured to be 2.53s. An irregularly shaped object, which we call object X, is then hung from the same wire, as in Fig. 15.13b, and its period $T_{b}$ is found to be 4.76s. What is the rotational inertia of object X about its suspension axis?

Text Solution

Verified by Experts

The rotational inertai of either the rod or object X is related to the measured period by Eq. 15.39.
Calculations: In Table 10-2e, the rotational inertia of a thin rod about a perpendicular axis through its mid point is given as $1 / 12 m L^{2}$ . Thus, we have, for the rod in Fig 15.16a,
$I_{a} - \frac{1}{12} m L^{2} = (\frac{1}{12}) (0.135 k g) {(0.124 m)}^{2}$
$= 1.73 \times 10^{- 4} k g m^{2}$

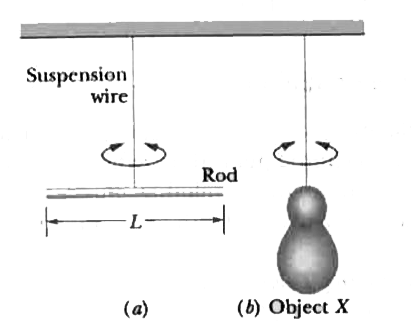
Now let us write Eq. 15.39 twice, once for the rod and once for object X:
$T_{a} = 2 π \sqrt{\frac{I_{a}}{k}} and T_{b} = 2 π \sqrt{\frac{I_{b}}{k}}$
The constant k, which is a property of the wire, is the same for both figures, only the periods and the rotational inertias differ.
Let us square each of these equations, divide the second by the first, and solve the resulting equation for $I_{b}$ . The result is
$I_{b} = I_{a} \frac{T_{b}^{2}}{T_{a}^{2}} = (1.73 \times 10^{- 4} k g . m^{2}) \frac{{(4.76 s)}^{2}}{{(2.53 s)}^{2}}$
$= 6.12 \times 10^{- 4} k g . m^{2}$

Updated on:21/07/2023