shows a Gaussian surface in the shape of a cube with edge length 5.60 m. What are (a) the net flux ϕ through the surface and (b) the net chargeqexc enclosed by the surface if→E=(3.00yˆj) N/C with y in meters? What are (c )ϕand(d)9cnc if →E=[−17.0ˆi+(6.00+3.00yˆj) N/C?
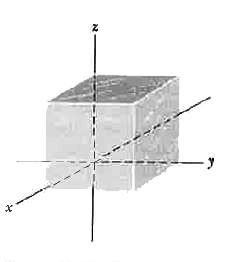
shows a Gaussian surface in the shape of a cube with edge length 5.60 m. What are (a) the net flux phi through the surface and (b) the net charge q(exc) enclosed by the surface ifvec E = (3.00 yhatj) N/C with y in meters? What are (c ) phi and (d) 9(cnc) if vecE =[-17.0hati +(6.00+ 3.00 yhatj) N/C?

Text Solution
Verified by Experts

(a)527N.m2/C,(b)4.66×10−9C(c)527N.m2/C,(d)4.66×10−9C

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12PHYSICSELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Figure above shows a closed Gaussian surface in the space of a cube of edge length 3.0m. There exists an electric field given by →E=[(2.0x+4.0)i+8.0j+3.0k]N/C, where x is in metres, in the region in which it lies. The net charge in coulumbs enclosed by the cube is equal to
    ocr_image

    A−54∈0
    B6∈0
    C−6∈0
    D54∈0

  • Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
    Electric flux, in general , through any surface is defined as per relation:
    ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
    A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
    A charge q is enclosed by a Gaussian spherical surface of raidus R. If the radius is doubled then the electric flux will.

    Abe doubled
    Bincreases four times
    Cbe reduced to half.
    Dremain the same.

  • Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
    Electric flux, in general , through any surface is defined as per relation:
    ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
    A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
    What is the electrical flux through a cube of side 'a' if a point charge 'q' is placed at one of its vertices?

    Aq∈0
    B2q∈0
    Cq8∈0
    Dq∈0.6a2