Figure above shows a closed Gaussian surface in the space of a cube of edge length 3.0m. There exists an electric field given by →E=[(2.0x+4.0)i+8.0j+3.0k]N/C, where x is in metres, in the region in which it lies. The net charge in coulumbs enclosed by the cube is equal to
![Figure above shows a closed Gaussian surface in the space of a cube of edge length 3.0m. There exists an electric field given by vec E= [(2.0x+4.0)i +8.0j +3.0k]N//C, where x is in metres, in the region in which it lies. The net charge in coulumbs enclosed by the cube is equal to](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_PHY_RK_JM_C19_E01_639_Q01.png)
−54∈0
6∈0
−6∈0
54∈0
The correct Answer is:D
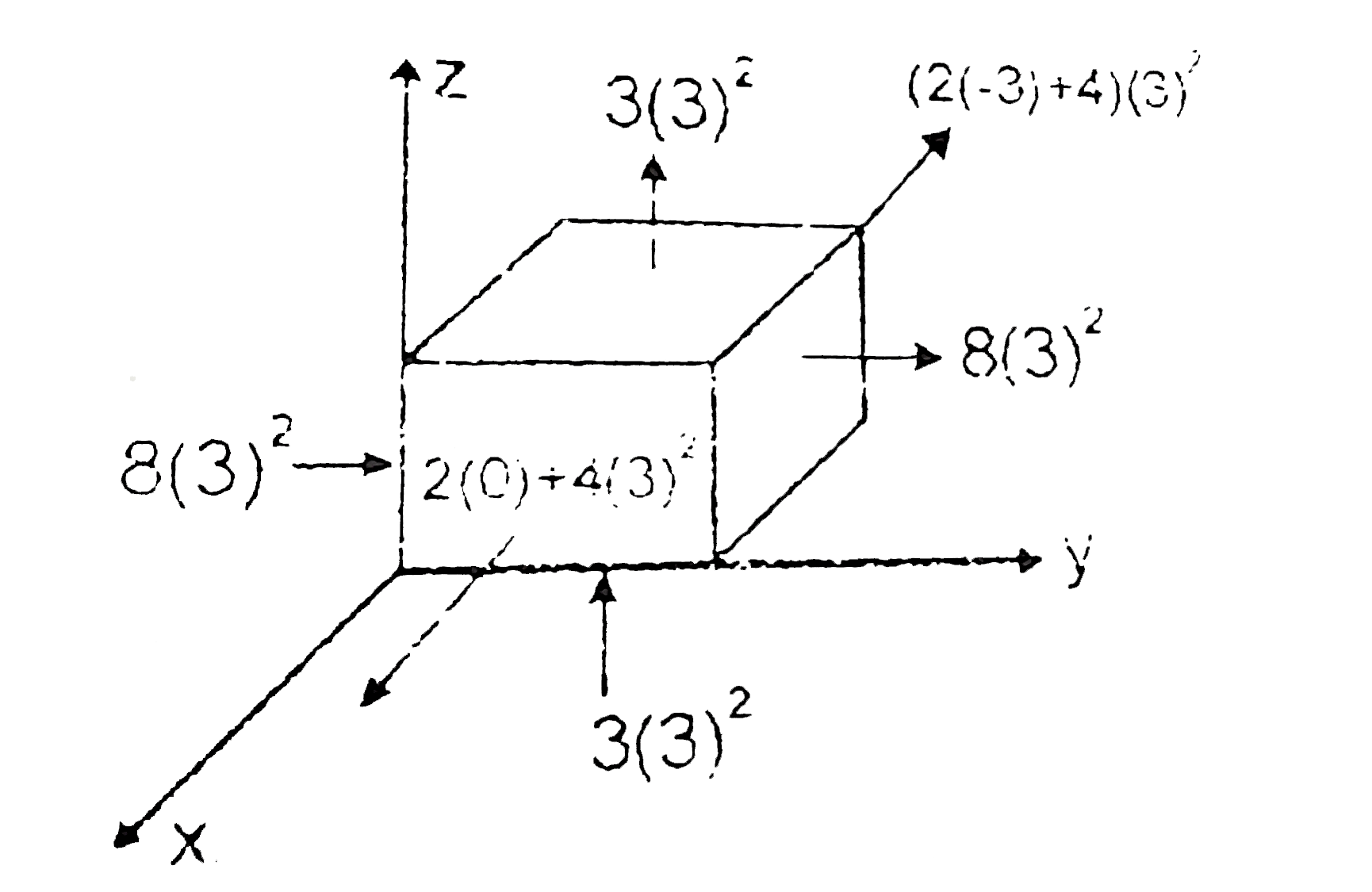
ϕ=∫→E.d→s
Direction of field at x = -3 m is along negative x axis. Area vector is also along same direction
ϕ=6×9=Qε0
Q=54∈0
Components of electric field which are constant
do not contribute in net flux in or out.
qin∈0=54⇒qin=54∈0
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.599videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.608videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.579videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
In the given electric field →E=[α(d+x)ˆi+E0ˆj]NC−1, where α=1NC−1 hypothetical closed surface is taken as shown in figure .
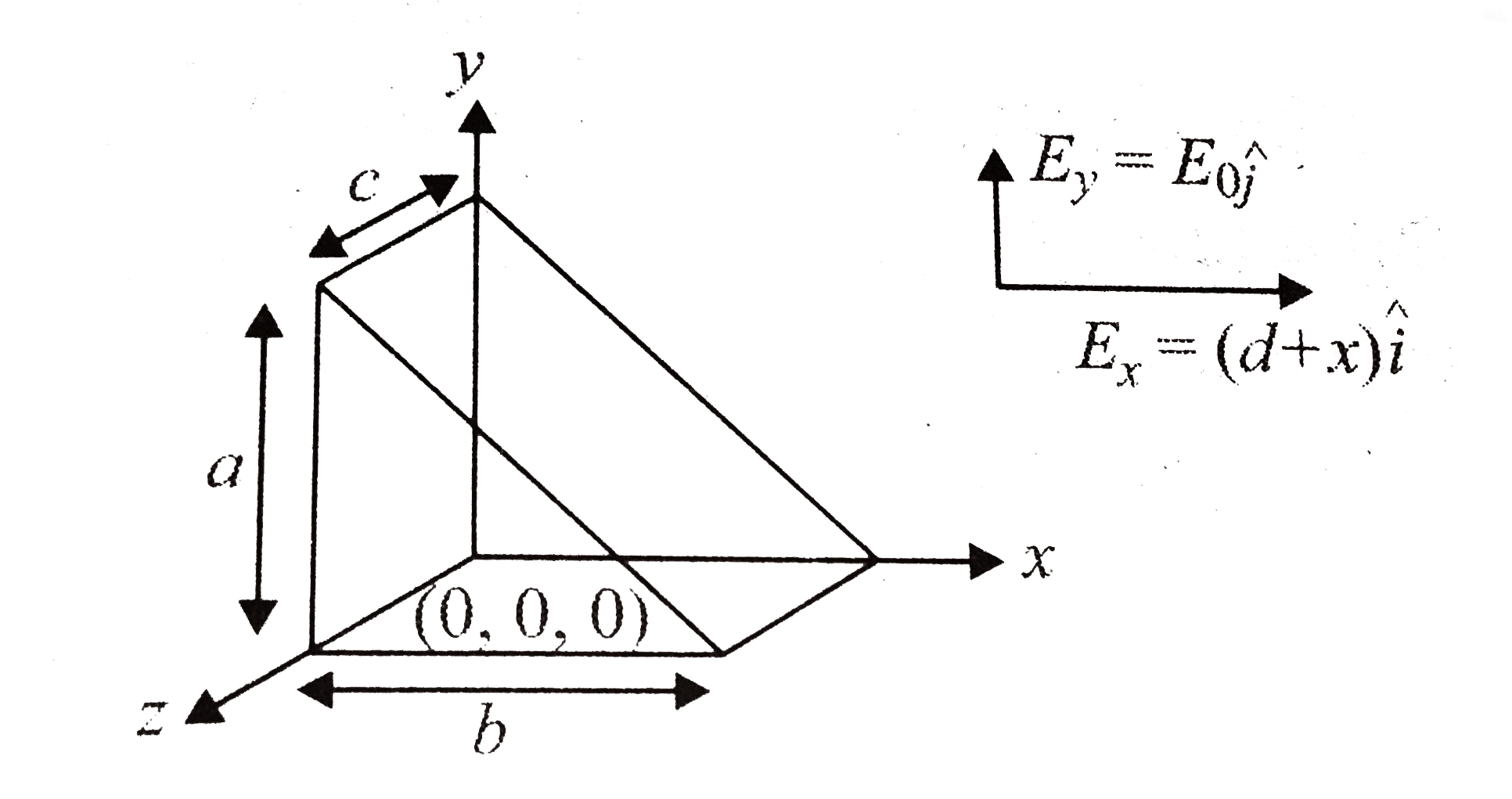
The total charge enclosed within the close surface isView SolutionA hollow cylindrical box of length 0.5m and area of cross-section 20cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by →E=20xˆi, where E is NC−1 and x is in meters, Find
(i) Net flux through the cylinder.
(ii) Charge enclosed in the cylinder.View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram
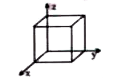View SolutionFind the area of the region enclosed by the given curves .
y=x3+3,y=0,x=−1,x=2View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0k. Total electric flux passing through the cube would be
View SolutionIf unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
View SolutionA cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.
View SolutionA solid insulating sphere of radius a carries a net positive charge 3Q, uniformly distributed throughout its volume. Concentric with this sphere is a conducting spherical shell with inner radius b and outer radius c and having a net charge -Q, as shown in figure
a. Consider a spherical Gaussian surface of radius rgtc, the net charge enclosed by this surface is .............
b. The direction of the electric field rgtc is .............
c. The electric field at rgtc is ............... .
d. The electric field in the region with radius r, which cgtrgtb, is ...............
e. Consider a spherical Gaussian surface of radius r, where c>r>b, the net charge enclosed by this surface is ................ .
f. Consider a spherical Gaussian surface of radius r, whereb>r>a, the net charge enclosed by this surface is ................. .
g. The electric field in the region b>r>a is ................ .
h. Consider a spherical Gaussian surface of radius r<a. Find an expression for the net charge Q(r) enclosed by this surface as a function of r. Note that the charge inside the surface is less than 3Q.
i. The electric field in the region r<a is ................. .
j. The charge on the inner surface of the conducting shell is .......... .
k. The charge on the outer surface of the conducting shell is .............. .
l. Make a plot of the magnitude of the electric field versus r.View SolutionIf electric field around a surface is given by ∣∣→E∣∣=Q∈ε0|A| where 'A' is the normal area of surface and Q∈ is the charge enclosed by the surface. This relation of gauss's law is valid when
View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. The charge enclosed in the cube of side 1m oriented as shown in the diagram is given by α∈0. Find the value of α.
View Solution