Question

(a) In Fig. 24-17 a, 12 electrons ( of charge $-e$ ) are equally spaced and fixed around a circle of radius R. Relative to $V=0$ at infinity, what are the electric potential and electric field at the center C of the circle due to these electrons?
(b) The electrons are moved along the circle until they are nonuniformly spaced over a 120° arc (Fig. 24-17b). At C, find the electric potential and describe the electric field.

Explanation

(1) The electric potential V at C is the algebraic sum of the electric potentials contributed by all the electrons. Because electric potential is a scalar, the orientations of the electrons do not matter. (2) The electric field at C is a vector quantity and thus the orientation of the electrons is important.
Calculations: Because the electrons all have the same negative charge `-e` and are all the same distance R from C, Eq. 24-29 gives us
`V=-12 (1)/(4 pi epsilon_(0)) (e )/( R)." "` (Answer) (24-30)
Because of the symmetry of the arrangement in Fig. 24-17 a, the electric field vector at C due to any given electron is canceled by the field vector due to the electron that is diametrically opposite it. Thus, at C,
`overset(to) (E ) =0`. (Answer)

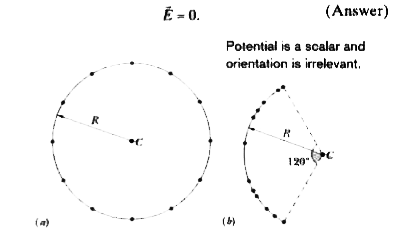
(b) Reasoning: The potential is still given by Eq. 24-30, because the distance between C and each electron is unchanged and orientation is irrelevant. The electric field is no longer zero, however, because the arrangement is no longer symmetric. A net field is now directed toward the charge distribution.