Figure 24-20 shows a thin plastic rod of length L = 12.0 cm and uniform positive charge Q=56.1 fC lying on the x axis. With V=0 at infinity, find the electric potential at point P1 on the axis, at distance d=2.50 cm of the rod.
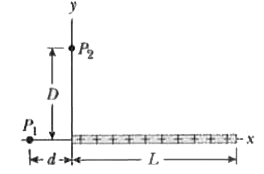
Consider an infinitesimal segment of the rod, located between x and x + dx. It has length dx and contains charge dq=λdx, whereλ=Q/L is the linear charge density of the rod. Its distance from P1 is d+x and the potential it creates at P1 is
dV=14πε0dqd+x=14πε0λdxd+x.
Finding potential To find the total potential at P1 , we integrate over the length of the rod and obtain:
V=λ4πε0∫L0dxd+x=λ4πε0ln(d+x)∣L0=Q4πε0Lln(1+Ld)
=(8.99×109N.m2/C2)(56.1×10−15C)0.12mln(1+0.12m0.025m)
=7.39×10−3V.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.11 Finding potential of charged disk
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.12 Potential due to infinite sheet of charge
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.09 Net potential due to two charged particles
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
The thin plastic rod of length L = 12.0 cm in Fig. 24-61 has a nonuniform linear charge density λ=cx, where c=49.9pC/m2. With V = 0 at infinity, find the electric potential at point P2 on the y axis at y = D = 3.56 cm. (b) Find the electric field component Ey at P2. (c) Why cannot the field component Ex at P2 be found using the result of (a) ?
View SolutionA rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric foeld at a point P located along the long axis of the rod and at a distance a from one end

View Solution
Knowledge Check
A charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
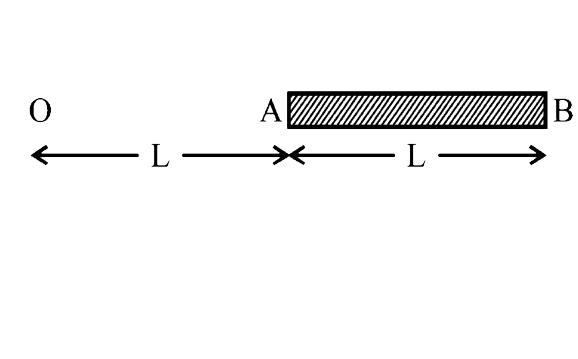 A(a) Q8πε0LB(b) 3Q4πε0LC(c) Q4πε0L1n2D(d) Q1n24πε0Ls
A(a) Q8πε0LB(b) 3Q4πε0LC(c) Q4πε0L1n2D(d) Q1n24πε0Ls
A rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric field at a point P located along the long axis of the rod and at a distance a from one end

View SolutionFigure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is λ. Find the electric field due to the rod at a point P which is at a distance r from the rod.
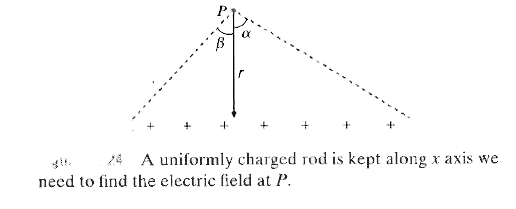
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionIn Fig., positive charge q = 9.25 pC is spread uniformly along a thin nonconducting rod of length L = 16.0 cm. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the electric field produced at point P, at distance R = 6.00 cm from the rod along its perpendicular bisector ?

View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is

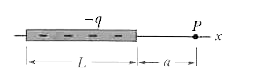
View SolutionIn Fig., a nonconducting rod of length L = 8.15 cm has a charge -q = -4.23 fC uniformly distributed along its length. (a) What is the linear charge density of the rod ? What are the (b) magnitude and (c ) direction (relative to the positive direction of the x axis) of the electric field produced at point P, at distance a = 6.00 cm from the rod ? What is the electric field magnitude produced at distance a = 50 m by (d) the rod and (e) a particle of charge -q = -4.23 fC that we use to replace the rod ? (At that distance, the rod "looks" like a particle.)
View Solution
