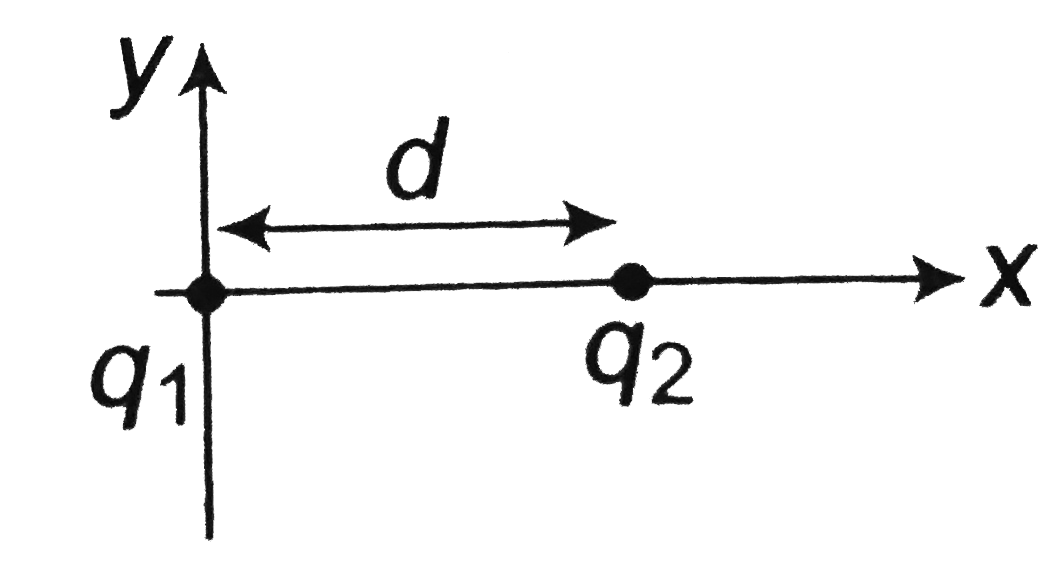
Two particles, of charges q1andq2, are separated by distance d in Fig. 24-18 with V = 0 at infinity.
(a) If the particles with charges q1=+5e and q2=−15e are fixed in place with a separation of d=24.0 cm, what are the finite (i) positive and (ii) negative values of x at which the net electric potential on the x axis is zero?

(b) If the net electric field due to the particles is zero at x = d/4, then locate (in terms of d) any point on the x axis ( other than at infinity) at which the electric potential due to the two particles is zero?
First, we observe that V (x) cannot be equal to zero for x > d. In fact V (x) is always negative for x > d. Now we consider the two remaining regions on the x axis: x < 0 and 0 < x < d.
(i) For 0 < x < d we have d1=xandd2=d−x . Let
V(x)=k(q1d1+q2d2)=q4πε0(1x+−3d−x)=0
and solve: x=d/4. With d=24.0 cm, we have x=6.00cm.
(ii) Similarly, for x < 0 the separation between q1 and a point on the x axis whose coordinate is x is given by d1=x: while the corresponding separation for q2 is d2=d−x. We set
V(x)=k(q1d1+q2d2)=q4πε0(1−x+−3d−x)=0
to obtain x=−d/2. With d=2.4 cm, we have x=−12.0 cm.
Since according to the problem statement there is a point in between the two charges on the x axis where the net electric field is zero, the fields at that point due to q1andq2 must be directed opposite to each other. This means that q1andq2 must have the same sign (i.e., either both are positive or both negative). Thus, the potentials due to either of them must be of the same sign. Therefore, the net electric potential cannot possibly be zero anywhere except at infinity.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.10 Potential due to line of charge
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.11 Finding potential of charged disk
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.08 Potential is not a vector, orientation is irrelevant
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
Two particles of charge q1 and q2 are separated by distance d as shown in figure. Chrage q1 is situarted at the origin. The net electirc field due to the particles is zero at x=d/4. With V=0 at infinity, the location of a point in terms of d on the x axis (other at infinfity) at which the elctrical potential due to the two particles is zero, is given by:
View SolutionTwo positive point charges q1=16μC and q2=4μC are separated in vacuum by a distance of 3.0m. Find the point on the line between the charges where the net electric field is zero.-
View Solution
Knowledge Check
Two particles of charge q1 and q2 are separated by distance d as shown in figure. Chrage q1 is situarted at the origin. The net electirc field due to the particles is zero at x=d/4. With V=0 at infinity, the location of a point in terms of d on the x axis (other at infinfity) at which the elctrical potential due to the two particles is zero, is given by:
 Ad/2B16dC−16dDno point on the x axis
Ad/2B16dC−16dDno point on the x axisTwo positive point charges q1=16μC and q2=4μC are separated in vacuum by a distance of 3.0m. Find the point on the line between the charges where the net electric field is zero.-
A2m from q1B1m from q1C2m from q2D0.5m from q1Two point charges q1=+2C and q2=−1C are separated by a distance d. The position on the line joining the two charges where a third charge q=+1C will be in equilibrium is at a distance
Ad√2 from q1 and q2Bd√2 from q1 away from q2Cd√2−1 from q2 between q1 and q2Dd√2−1 from q2 away from q1
Two point charges q1 and q2 are fixed at a separation of 20 cm. Locate the point(s) on the line joining the charges where the net electric field intensity is zero.
(i)q1=+2μC and q2=−4μC
(ii)q1=+2μC and q2=−2μC
(iii)q1=+2μC and q2=+4μC
View SolutionTwo charge Q1=18μC and Q2=−2μC are separated by a distance R, and Q1 is on the left of Q2. The distance of the point where the net electric field is zero is
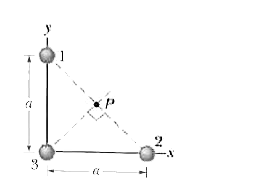
View SolutionIn Fig., the three particles are fixed in place and have charges q1=q2=+5e and q3=+2e. Distance a=3.00μm. What are the (a) magnitude and (b) direction of the net electric field at point P due to the particles ?
View SolutionTwo point charges, q1=10×10−8Candq2=−2×10−8C, are separated by a distance of 60 cm in air.
Find at what distance from the 1st charge q1, would the electric potential be zero.
View SolutionIn Fig. 22-19, particle 1 of charge q1=5.00q and a particle 2 of charge q2+2.00q are fixed on the x-axis.
As a multiple of distance L, at what coordinate on the axis is the net electric field of the particles zero?

View Solution
