A plastic disk of radius R = 64.0 cm is charged on one side with a uniform surface charge density , and then three quadrants of the disk are removed. The remaining quadrant is shown in Fig. 24-22. With V = 0 at infinity, what is the potential due to the remaining quadrant at point P, which is on the central axis of the original disk at distance D = 25.9 cm from the original center?

Since the disk is uniformly charged, when the full disk is present each quadrant contributes equally to the electric potential at P.
Expressing potential: Electrical potential is a scalar quantity. The potential at P due to a single quadrant is one-fourth the potential due to the entire disk. We first find an expression for the potential at P due to the entire disk. To do so, consider a ring of charge with radius and (infinitesimal) width dr. Its area is and it contains charge . All the charge in it is at a distance from , so the potential it produces at P is
Calculation: Integrating over , the total potential at is
.
Therefore, the potential at P due to a single quadrant is
.
Learn: Consider the limit . The potential becomes
where is the charge on the quadrant. In this limit, we see that the potential resembles that due to a point charge .
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.12 Potential due to infinite sheet of charge
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.13 Potential at the surface of the outer shell
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.10 Potential due to line of charge
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
A uniform disc of radius R is charged with a uniform surface charge density σ. Find the electric potential due to the charges on the disc at a point on its edge. [σRπ∈0]
View SolutionAn annular disc of inner radius a and outer radius '2a' is uniformly charged with uniform surface charge density σ. Find the potential at a distance 'a' from the centre at a point 'P' lying on the axis.
View Solution
Knowledge Check
A circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
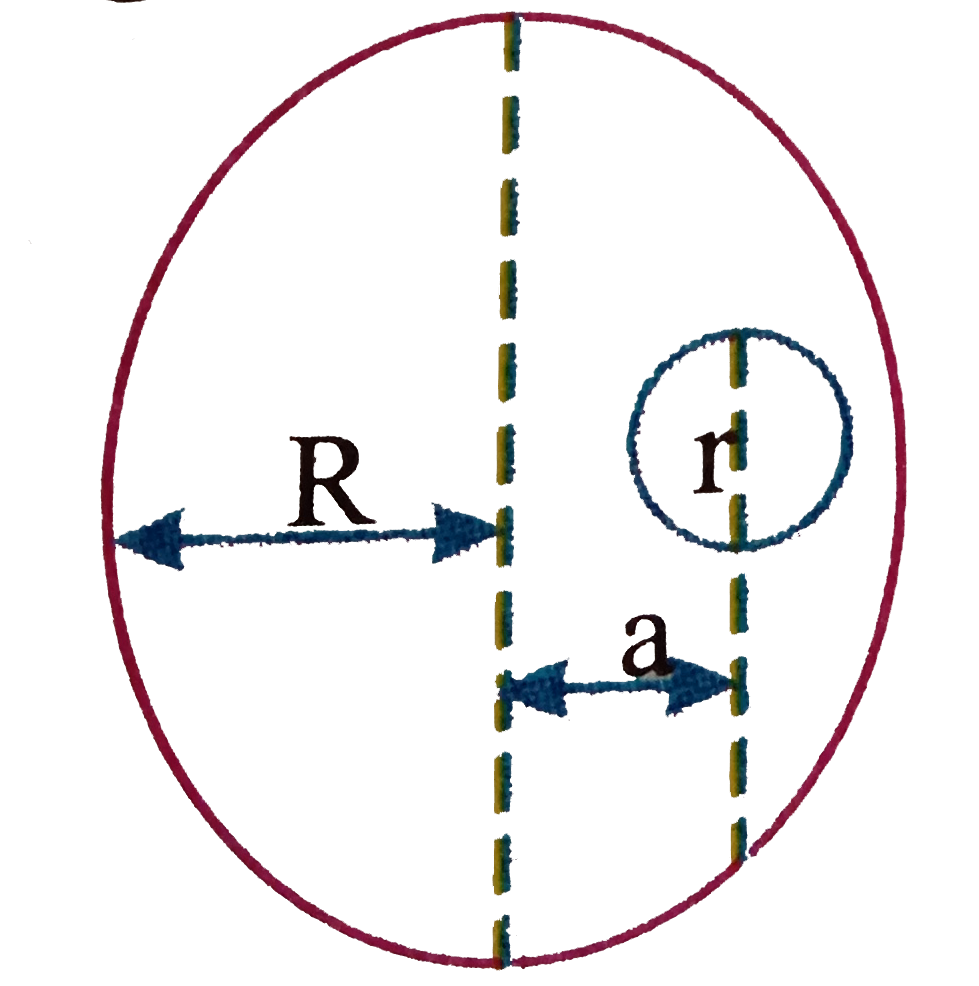 AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2
AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2For the hemisphere of radius R shown in the figure the surface charge density σ varies with θ (shown in figure) as σ=σ0cosθ the total charge on the sphere is
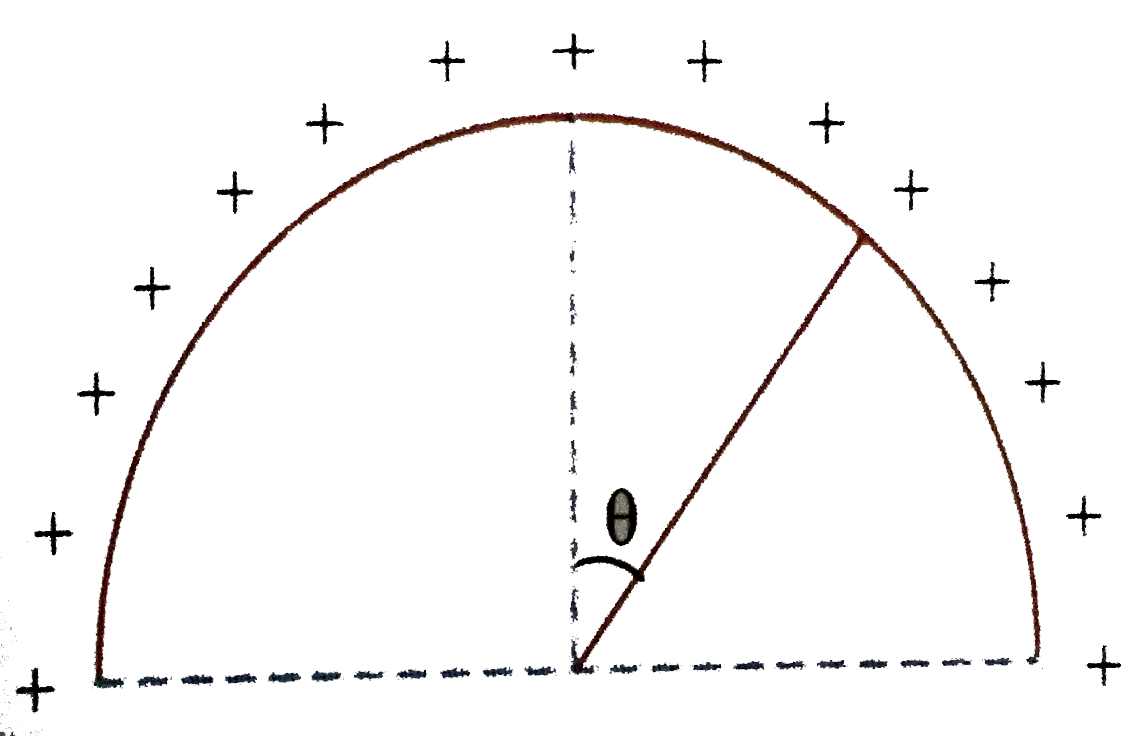 A2σ0πR2Bσ0πR22Cσ0πR23Dσ0πR2
A2σ0πR2Bσ0πR22Cσ0πR23Dσ0πR2A copper disk of radius 0.1m is rotated about its center with 200 rev/s in uniform magnetic field. Induced emf across the radius of the disc is:
Aπ20VBπ100VC20πmVD0
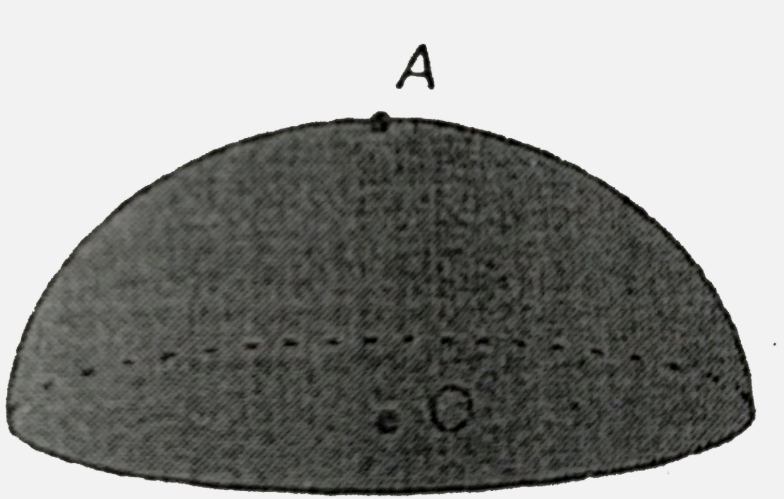
A hemispherical bowl of radius R carries a uniform surface charge density σ. Find the potential at the topmost point A, taking potential at infinity to be zero.
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending upto infinity in the first quadrant of x-y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the points (0,0,d) & (0,0,2d).
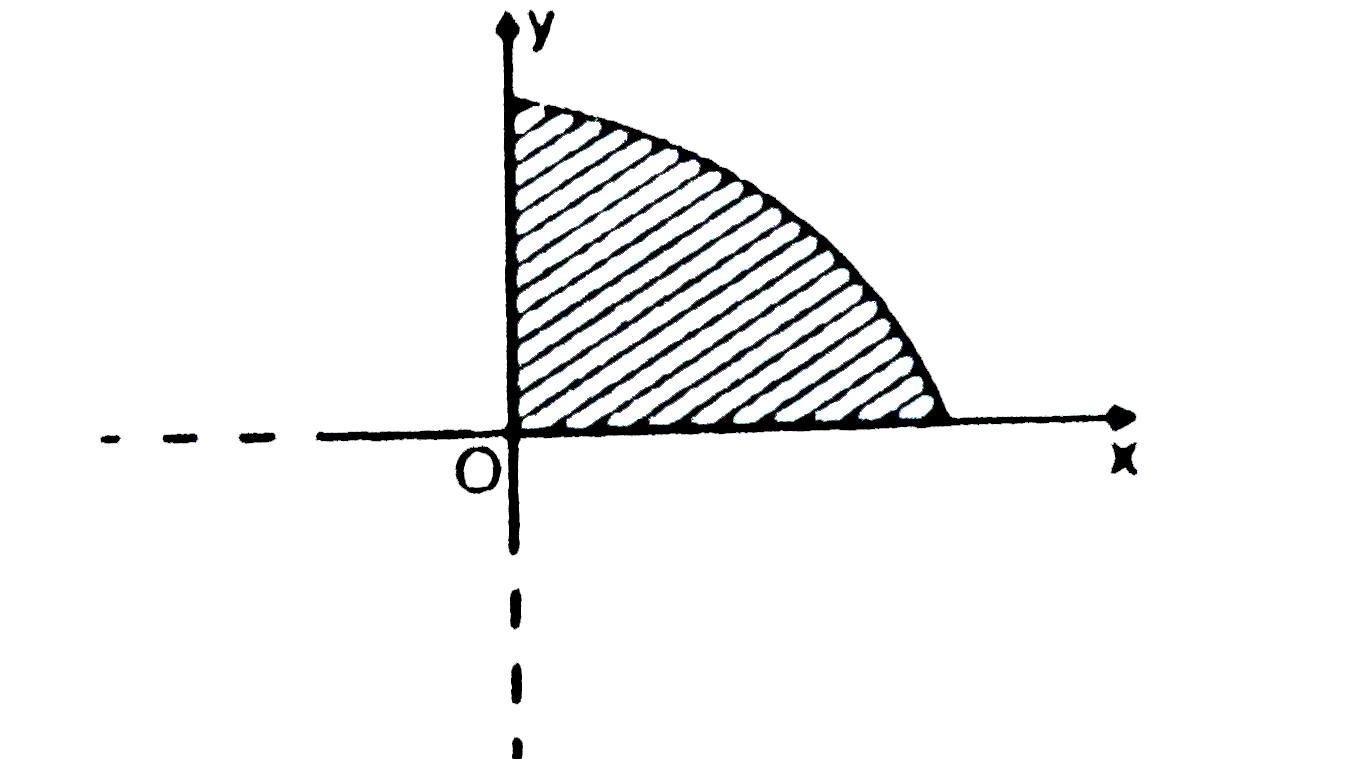
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending upto infinity in the first quadrant of x-y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the points (0,0,d) & (0,0,2d).

View SolutionIn the given figure, PQR is a quadrant whose radius is 7 cm. A circle is inscribed in the quadrant as shown in the figure. What is the area (in cm2) of the circle

View SolutionA thin circular disk of radius R is uniformly charged with density σ>0 per unit area.The disk rotates about its axis with a uniform angular speed ω.The magnetic moment of the disk is :
View Solution
