A dipole of dipole moment p is placed at origin along x axis. Another dipole of dipole moment also p is kept at (0, 1, 0) along y axis. Find the resultant potential and electric field at (1, 0, 0).

Text Solution

Verified by Experts

We have studied that the electric field and potential both obey the law of superposition. We can find the electric field and the potential due to each of the dipole at the point concerned and then add them. The caution to be exercised is that while finding the electric field/potential due to a given dipole, we need to consider the center of that dipole as the origin.
Calculation: Due to the first dipole at the origin, the potential is
$V_{1} = \frac{k p cos θ}{r^{2}} = \frac{k p}{1^{2}} = k p$
Due to the second dipole at y = 1, the potential is
$V_{2} = \frac{k p cos θ}{r^{2}} = \frac{k p}{{\sqrt{2}}^{2}} {cos 135}^{\circ} = \frac{k p}{2 \sqrt{2}}$
Therefore,
$V = V_{1} + V_{2} = k p - \frac{k p \sqrt{2}}{4}$ . (Answer)
Similarly, the electric field in the radial direction due to the first dipole is
$E_{r 1} = \frac{2 k p cos 0}{r^{3}} ˆ i = 2 k p ˆ i$ .
Here, the radial direction is also the x direction as can be seen from Fig. 24-35.
$E_{p 1} = \frac{2 k p sin 0}{r^{3}} ˆ j = 0 ˆ j$ .

Here, the polar direction is the positive y direction.
The magnitude of the electric field in the radial direction due to the second dipole is
$- cos 45 ˆ i - sin 45 ˆ j E_{r 2} = \frac{2 k p}{2 \sqrt{2}} {cos 135}^{\circ} = - \frac{k p}{2} .$
Here, the radial direction is shown in Fig. 24-36. A unit vector in the radial direction will be cos $45 ˆ i - sin 45 ˆ j$ . So,
$E_{r 2} = - \frac{k p}{2} (\frac{ˆ i}{\sqrt{2}} - \frac{ˆ j}{\sqrt{2}}) .$
Similarly, the electric field in the polar direction will be given by
$- - \to E_{p 2} = \frac{k p {sin 135}^{\circ}}{{(\sqrt{2})}^{3}} (- \frac{ˆ i}{\sqrt{2}} - \frac{ˆ j}{\sqrt{2}})$ .

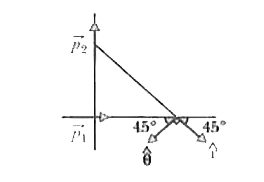
Because a unit vector in polar direction will be $- cos 45 ˆ i - sin 45 ˆ j$ , so we have
$\to E = 2 k p ˆ i - \frac{k p}{2 \sqrt{2}} ˆ i + \frac{k p}{2 \sqrt{2}} ˆ j - \frac{k p}{4 \sqrt{2}} ˆ j - \frac{k p}{4 \sqrt{2}} ˆ i - \frac{k p}{4 \sqrt{2}} ˆ j$
$= ⎛ ⎜ ⎜ ⎝ \frac{k p (8 \sqrt{2} - 3) ˆ i}{4 \sqrt{2}} + \frac{k p ˆ j}{4 \sqrt{2}} ⎞ ⎟ ⎟ ⎠ .$ (Answer)

Updated on:21/07/2023

Two short dipoles, each of diple moment p , are placed at origin. The dipole moment of one dipole is along x-axis, while that of other is along y-axis . The electric field at a point (a,0) is given by
A $(\frac{1}{4 π ε_{0}}) \frac{2 p}{a^{3}}$
B $(\frac{1}{4 π ε_{0}}) \frac{p}{a^{3}}$
C $(\frac{1}{4 π ε_{0}}) \frac{\sqrt{5} p}{a^{3}}$
DZero
An electric dipole of dipole moment p is placed in a uniform external electric field E. Then, the
Atoeque experienced by the dipole is $E \times p$
Btorque is zero, if p is perpendicular to E
Ctorque is maximum, if p is perpendicular to E
Dpotential energy is maximum, if p is parallel to E
A dipole of dipole moment $P$ is kept at the centre of a ring of radius $R$ and charge $Q$ the dipole moment has direction along the ring due to the dipole is :
Azero
B $\frac{k p Q}{R^{3}}$
C $\frac{2 k p Q}{R^{3}}$
D $\frac{k p Q}{R^{3}}$ only if the change is uniformly distributed on the ring .