Find the potential at point A due to (a) charge Q, ( b) charge on the outer surface of the conducting shell, and (c) total potential at A (Fig. 24-45).
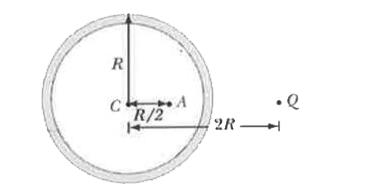
It is easy to find the potential due to a point charge. But the charge on the surface of the conducting shell is nonuniform and its potential can be tricky. However, we can use the fact that the entire conductor is an equipotential surface.
Calculation: The first part, potential due to Q is easy. It can be seen that
VQ=q6πε0R
There are induced charges on outer surface of the shell As discussed before, they are nonuniformly distributed. So, we cannot calculate the potential due to a nonuniform shell at A. But let us try to calculate the potential due to this shell at C, the center of the shell. We cannot use the formula for the uniformly charged shell, but the center is equidistant from all the induced charges at the surface. Since potential is a scalar, Vat the center due to the induced charges will be
VCin=∑qin4πε0R.
Since the shell is initially uncharged, the total charge on it will be zero. o, the potential at C due lo induced charges will be zero. Therefore, the total potential at C will be
Vcq+Vc in=Q8πε0R+0.
As we discussed before, the potential at all the points within the cavity should be the same. So, VA=VC
From this, we can say that
VA=QQπε0R
VA=VAQ+V A in=Q8πε0R
V A in =−Q24πε0R.
Learn: We can see why the potential at A is negative. The induced charges near Q will be negative, and equal and opposite charges will be induced on the other side of the conductor. They will be farther off, producing a net negative potential at A.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.24 Potential due to charges on three concentric shells
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.25 Charge and potential on a conductor that is earthed
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.22 Conservation of mechanical energy with electric potential energy
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
Find an expression for the potential at a point due to a point charge Q.
View Solution
A point charge q'q is placed at distance 'a' from the centre of an uncharged thin spherical conducting shell of radius R=2a. A point 'P' is located at a distance 4a from the centre of the conducting shell as shown. The electric potential due to induced charge on the inner surface of the conducting shell at point 'P' is
View Solution
Knowledge Check

A point charge q'q is placed at distance 'a' from the centre of an uncharged thin spherical conducting shell of radius R=2a. A point 'P' is located at a distance 4a from the centre of the conducting shell as shown. The electric potential due to induced charge on the inner surface of the conducting shell at point 'P' isAkq5aB−kq5aCkq4aD−kq4aA solid conducting sphere, having a charge Q, is surrounded by an uncharged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a charge of -4 Q, the new potential difference between the same two surfaces
A4 VB2 VC−2VDVA solid conducting sphere having a charge Q is surrounded by an uncharged concentric conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a charge of −3Q, the new potential difference between the same two surfaces is :
A(a) VB(b) 2VC(c) 4VD(d) −2V
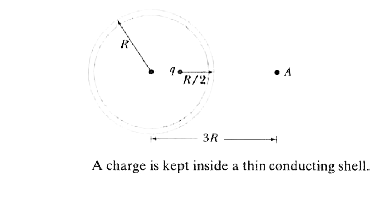
Find the electric field at (A) (a) due to q, (b) due to charges induced on the inner surface of the shell and (c ) due to charges induced on the outer surface of the shell (Fig. 22-41).
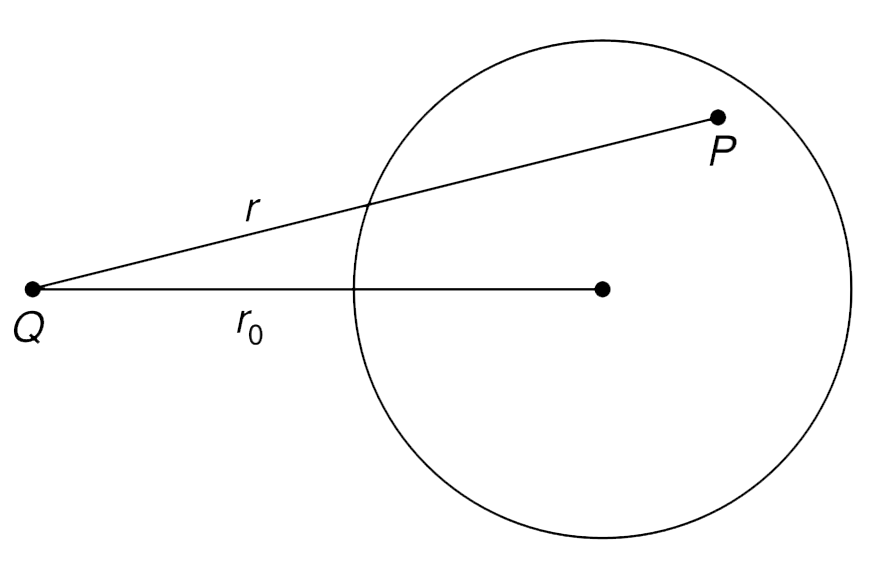
View SolutionA conducting shell having no charge has radius R. A point charge Q is placed in front of it at a distance r0 from its centre. Find potential due to charge induced on the surface of the shell at a point P inside the shell. Distance of point P from point charge Q is r.
View SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2.
Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionA solid conducting sphere, having a charge Q, is surrounded by an unchanged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a change of −4Q, the new potential difference between the same tow surface is :
View SolutionIn an arrangement of two concentric conducting shells, with centre at origin and radii a and b (a<b), charges Q1 and Q2 are given to inner and outer shell, then the potential V at a distance r from the origin is (r<a)
View Solution
