Assume that two spherical concentric conducting shells of radius randR are kept as shown in Fig. 24-53. The inner shell is given a charge Q and the outer shell is earthed. Find the charge supplied by the Earth and the potential of the inner shell.

Let q be the charge given by the Earth. Note that when the body is connected to Earth, its charge will not be conserved. Some amount of charge can flow from the Earth or flow to the Earth to make its potential zero. The body which is not connected to the Earth will retain its original charge.
Calculation: Potential at surface of outer shell:
Q4πε0R+q4πε0R=0.
So, q=−Q. So, the Earth has to supply a charge of −Q to make the potential of the outer shell zero. But the potential of inner shell need not be zero.
Vin=Q4πε0r−Q4πε0R.
This potential will be positive.
Learn: Another interesting point that we can note here is that since the shells are conducting, the charge −Q will reside on the inner surface of the outer shell. So, the charge on the outer surface of the shell will be zero!
Can you guess why! Let us recall that the joining of the outer shell to the Earth brings both the Earth and the shell at the same potential. So, the electric field between the Earth and the outer shell will be zero. This is possible only if the charge on the outer surface of shell is zero. The charge inside the cavity cannot produce any electric field outside because electric field lines cannot penetrate a conductor.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.26 Self-energy of a uniformly charged sphere
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.27 Electrostatic energy of two charged conducting shells, with and without earthing
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.24 Potential due to charges on three concentric shells
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
In (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View SolutionIn (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View Solution
Knowledge Check
Two thin conducting shells of radii R and 3R are as shown in the fig. External shell carries a charge +Q and inner shell neutral. The inner shell is earthed with the help of a switch S. Then
 Awith the switch S open, the potential of the inner sphere is equal to that of the outerBwith the switch S is closed, the potential of the inner spehre is becomes zeroCwith the switch S closed, the charge attained by the inner sphere is −Q/3DBy closing the switch the capacitance of the system increases
Awith the switch S open, the potential of the inner sphere is equal to that of the outerBwith the switch S is closed, the potential of the inner spehre is becomes zeroCwith the switch S closed, the charge attained by the inner sphere is −Q/3DBy closing the switch the capacitance of the system increasesIn the figure two concentric conducting shells of radius R & 2R are shown. The inner shell is charged with Q and the shell is unchanged. The amount of energy dissipated when the shells are connected by a conducting wire is:
 AKQ24RBkQ22RCkQ28RD3kQ24
AKQ24RBkQ22RCkQ28RD3kQ24
Two thin conducting shells of radii R and R ar shown in figure . The outer shell carries a charge +Q and the inner shell is neutral. The inner shell is earthed with the help of switch S . Find the charge attained by the inner shell.
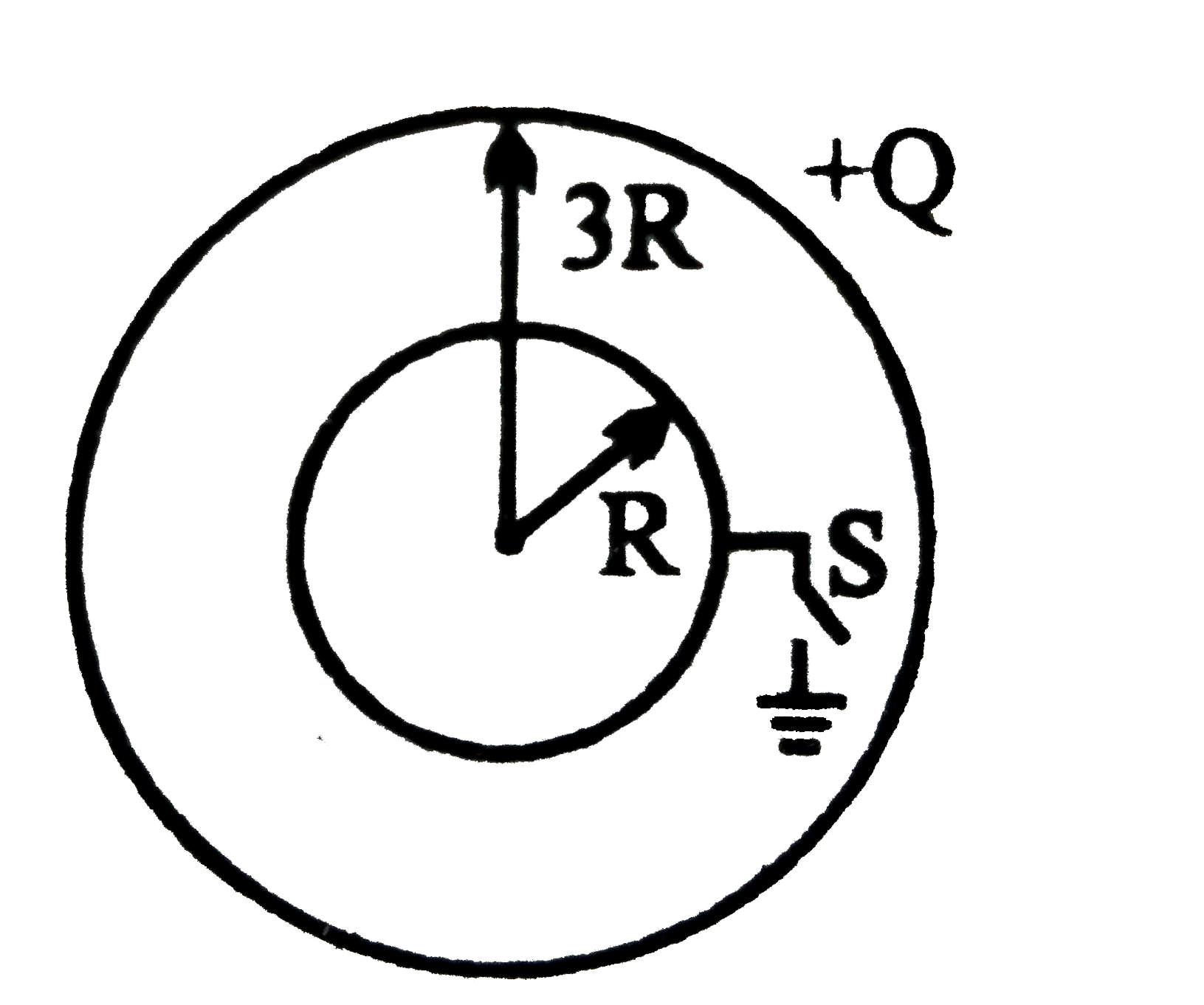 .
.
View SolutionTwo thin conducting shells of radii R and 3R are as shown in the fig. External shell carries a charge +Q and inner shell neutral. The inner shell is earthed with the help of a switch S. Then

View SolutionThere are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View SolutionThere are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View SolutionThere are two concentric conducting spherical shells of radii 10 cm and 20 cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionThere are two concentric conducting spherical shells of radii 10cm and 20cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View Solution
