Flux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)

q/ε0
q/2ε0
q/4ε0
zero
The correct Answer is:C
α=60∘ . Solid angle subtended by BCD is
Solid angle subtended by ABCD is
ω(ABCDE)−ω(BCD)=2π−π=π
Hence , flux through ABDE is
ϕ=qε0π4π=q4ε0

Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator
24 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator
24 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE -2 : CONCEPT ALLPLICATOR
30 Videos
- ELECTROMAGNETIC INDUCTION BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 2 : Concept Applicator
29 Videos
Similar Questions
A hollow non conducting sphere of radius R has a positive charge q uniformly distributed on its surface. The sphere starts rotating with a constant angular velocity 'ω' about an axis passing through center of sphere, as shown in the figure. Then the net magnetic field at center of the sphere is

View SolutionCharge is distributed uniformly in some space. The net flux passing through the surface of an imaginary cube of side a in the space is ϕ. The net flux passing through the surface of an imaginary sphere of radius a in the space will be
View Solution
Knowledge Check
A hollow non conducting sphere of radius R has a positive charge q uniformly distributed on its surface. The sphere starts rotating with a constant angular velocity 'ω' about an axis passing through center of sphere, as shown in the figure. Then the net magnetic field at center of the sphere is
 Aμ0qω2πRBμ0qω3πRCμ0qω6πRDμ0qω12πR
Aμ0qω2πRBμ0qω3πRCμ0qω6πRDμ0qω12πRCharge is distributed uniformly in some space. The net flux passing through the surface of an imaginary cube of side a in the space is ϕ. The net flux passing through the surface of an imaginary sphere of radius a in the space will be
AϕB34πϕC2π3ϕD4π3 phiA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
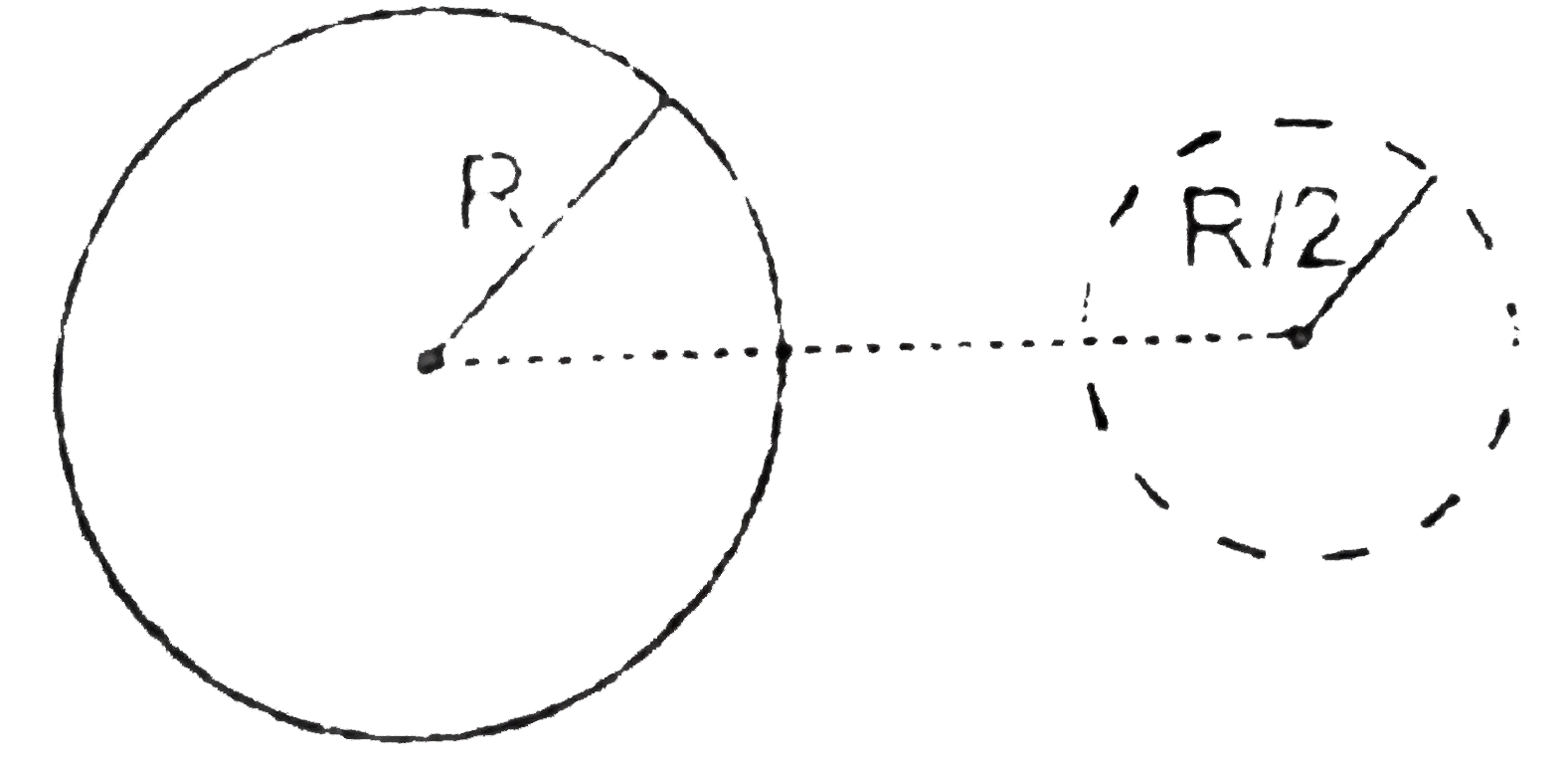 AλR∈0BλR2∈0CλπR4∈0DλπR3∈0
AλR∈0BλR2∈0CλπR4∈0DλπR3∈0
Charge is distributed uniformly in some space. The net flux passing through the surface of an imaginary cube of side a in the space is ϕ. The net flux passing through the surface of an imaginary sphere of radius a in the space will be
View SolutionFigure shown a closed surface which intersects a conducting sphere. If a positive charge is placed at the point P, the flux of the electric field through the closed surface

View SolutionA point charge is placed at the centre of spherical Gaussian surface. Is electric flux ϕE changed if
(a) The sphere is replaced by a cube of same or different volume ?
(b) The charge is moved off-centre in the original sphere, still remaining inside ?
( c ) The charge is moved just outside the original sphere ?
(d) A second charge is placed near the outside to the origianl schere ?
(e) A second charge is placed inside the Gaussian surface ?
View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is

View SolutionIf a point charge is placed at vertex of cube then flux linked to surface shaded in figure a
View Solution
