The magnetic field of a cylindrical magnet that has a poleface diameter of 3.3 cm can be varied sinusoidally between 29.6 T and 31.2 T at a frequency of 15 Hz. (The current in a wire wrapped around a permanent magnet is varied to give this variation in the net field.) At a radial distance of 1.6 cm, what is the amplitude of the electric field induced by the variation?
To solve the problem, we will follow these steps:
Step 1: Determine the parameters of the magnetic field
- The magnetic field varies between Bmin=29.6T and Bmax=31.2T.
- The amplitude of the magnetic field variation BA is calculated as:
BA=Bmax−Bmin2=31.2T−29.6T2=0.8T
Step 2: Calculate the average magnetic field B0
- The average magnetic field B0 is given by:
B0=Bmax+Bmin2=31.2T+29.6T2=30.4T
Step 3: Identify the radial distance
- The radial distance at which we want to find the electric field is r=1.6cm=0.016m.
Step 4: Calculate the angular frequency ω
- The frequency f is given as 15Hz.
- The angular frequency ω is calculated using the formula:
ω=2πf=2π×15Hz=30πrad/s
Step 5: Use Faraday's law of electromagnetic induction
- According to Faraday's law, the induced electric field E in a cylindrical region is given by:
E=−r2dBdt
- The time derivative of the magnetic field B can be expressed as:
dBdt=BAωcos(ωt)
- Therefore, substituting BA and ω:
E=−r2BAωcos(ωt)
Step 6: Calculate the amplitude of the electric field
- The amplitude of the electric field Emax occurs when cos(ωt)=1:
Emax=r2BAω
- Substituting the values:
Emax=0.016m2×0.8T×30πrad/s
- Calculating:
Emax=0.008×0.8×30π=0.192π≈0.603V/m
Final Result
The amplitude of the electric field induced by the variation at a radial distance of 1.6 cm is approximately:
Emax≈0.6V/m
---
- The magnetic field varies between Bmin=29.6T and Bmax=31.2T.
- The amplitude of the magnetic field variation BA is calculated as:
BA=Bmax−Bmin2=31.2T−29.6T2=0.8T
- The average magnetic field B0 is given by:
B0=Bmax+Bmin2=31.2T+29.6T2=30.4T
- The radial distance at which we want to find the electric field is r=1.6cm=0.016m.
- The frequency f is given as 15Hz.
- The angular frequency ω is calculated using the formula:
ω=2πf=2π×15Hz=30πrad/s
- According to Faraday's law, the induced electric field E in a cylindrical region is given by:
E=−r2dBdt
- The time derivative of the magnetic field B can be expressed as:
dBdt=BAωcos(ωt)
- Therefore, substituting BA and ω:
E=−r2BAωcos(ωt)
- The amplitude of the electric field Emax occurs when cos(ωt)=1:
Emax=r2BAω
- Substituting the values:
Emax=0.016m2×0.8T×30πrad/s
- Calculating:
Emax=0.008×0.8×30π=0.192π≈0.603V/m
The amplitude of the electric field induced by the variation at a radial distance of 1.6 cm is approximately:
Emax≈0.6V/m
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)45videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)13videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS9videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type1videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)7videos
ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT
Similar Questions
The magnetic field of a cylindrical magnet that has a pole face radius 2.8cm can be varied sinusoidally between the minimum value 16.8T and the maximum value 17.2T at a frequency of 50/πHz. Cross section of the magnetic field created by the magnet is shown in Fig. 3.211. At a radial distance of 2cm from the axis, find the amplitude of the electric field (∈unitsof×102mNC−1) induced by the magnetic field variation.
 View Solution
View SolutionIn a plane electromagnetic wave, magnetic field oscillates with amplitude1.6×10−11T Find the maximum value of electric field.
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic field of a cylindrecal magnet that has a pole − face radius 2.8cm can be varied sinusoidally between minimum value 16.8T and maximum value 17.2T at a frequecy of 60πHz. Cross section of the magnetic field created by the magnet is shown. At a radial distance of 2cm from the axis find the amplitude of the electric field (in mN/C ) induced by the magnetic field variation.
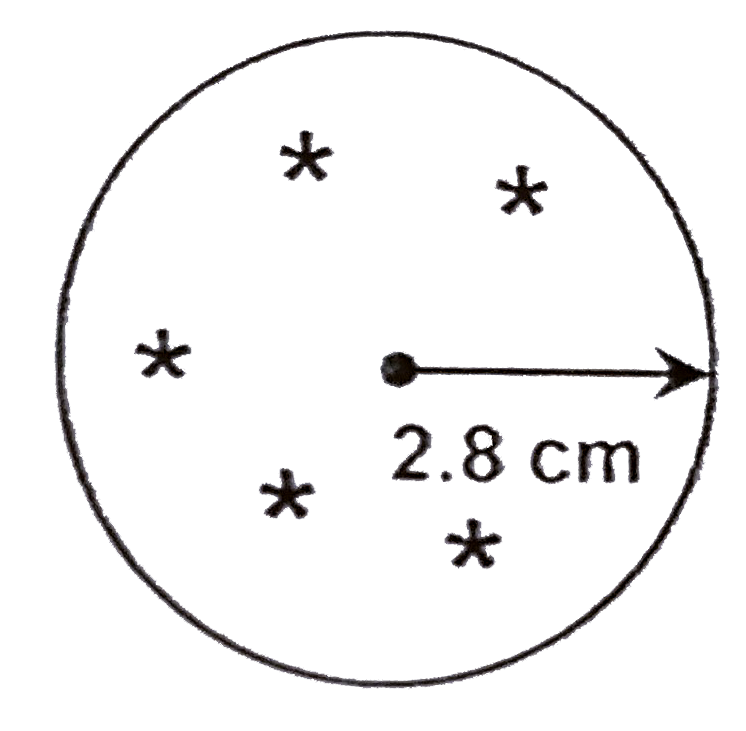 A140mN/CB245mN/CC180mN/CD240mN/C
A140mN/CB245mN/CC180mN/CD240mN/C - Question 2 - Select One
At a distance of 10 cm from a long staright wire carrying a current I, the magnetic field is 0.04 T. At a distance of 40 cm from the wire, the magnetic field will be
A0.01TB0.04TC0.16TD0.02T - Question 3 - Select One
At a distance of 10 cm from a long straight wire carrying current the magnetic field is 0.04 T. At the distance of 20 cm, the magnetic field will be
A0.01TB0.02TC0.08TD0.16T
A wire of length 3 cm has current 1 amp. Find magnetic field at a perpendicular distance a cm from centre of wire
 View Solution
View SolutionA 70 turn coil with average diameter of 0.02 m is placed perpendicular to magnetic field of 9000 T. If the magnetic field is changed to 6000 T is 3s, what is the magnitude of induced emf ?
View SolutionIn a plane e.m. wave, the electric field varies with time having an amplitude 1Vm−1. The frequency of wave is 0.5×1015Hz. The wave is propagating along Z-axis. What is the average energy density of (i) electric field (ii) magnetic field (iii) total (iv) what is the amplitude of magnetic field?
View SolutionAt a distance of 10cm from a long straight wire carrying current, the magnetic field is 0.04T. At the distance of 40cm, the magnetic field will be
View SolutionIn an electromagnetic wave, the amplitude of magnetic field is 3×10−10T. If the frequency of the waves is 1012Hz , then the amplitude of the associated electrical field will be :-
View Solution

