The current in an RL circuit drops from 2.30 A to 3.40 mA in 0.025 s following removal of the battery from the circuit. If L is 10 H, find the resistance R in the circuit.
To solve the problem of finding the resistance R in the RL circuit, we will follow these steps:
Step 1: Identify the given values
- Initial current I0=2.30A
- Final current I=3.40mA=3.40×10−3A
- Time t=0.025s
- Inductance L=10H
Step 2: Use the formula for current in an RL circuit
The current in an RL circuit after the battery is removed can be described by the equation:
I=I0e−tτ
where τ (the time constant) is given by:
τ=LR
Step 3: Rearrange the equation
We can rearrange the equation to express it in terms of R:
II0=e−tτ
Taking the natural logarithm on both sides:
ln(II0)=−tτ
Step 4: Substitute τ
Substituting τ=LR into the equation gives:
ln(II0)=−tRL
Step 5: Solve for R
Rearranging the equation to solve for R:
R=−Lln(II0)t
Step 6: Substitute the known values
Now, substitute the known values into the equation:
R=−10H⋅ln(3.40×10−32.30)0.025
Step 7: Calculate the logarithm
First, calculate the fraction:
3.40×10−32.30≈0.001478
Now, calculate the natural logarithm:
ln(0.001478)≈−6.525
Step 8: Substitute back into the equation
Now substitute this back into the equation for R:
R=−10⋅(−6.525)0.025
R=65.250.025=2610Ω
Step 9: Final answer
Thus, the resistance R in the circuit is approximately:
R≈2610Ω
- Initial current I0=2.30A
- Final current I=3.40mA=3.40×10−3A
- Time t=0.025s
- Inductance L=10H
The current in an RL circuit after the battery is removed can be described by the equation:
I=I0e−tτ
where τ (the time constant) is given by:
τ=LR
We can rearrange the equation to express it in terms of R:
II0=e−tτ
Taking the natural logarithm on both sides:
ln(II0)=−tτ
Substituting τ=LR into the equation gives:
ln(II0)=−tRL
Rearranging the equation to solve for R:
R=−Lln(II0)t
Now, substitute the known values into the equation:
R=−10H⋅ln(3.40×10−32.30)0.025
First, calculate the fraction:
3.40×10−32.30≈0.001478
Now, calculate the natural logarithm:
ln(0.001478)≈−6.525
Now substitute this back into the equation for R:
R=−10⋅(−6.525)0.025
R=65.250.025=2610Ω
Thus, the resistance R in the circuit is approximately:
R≈2610Ω
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS
9 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
The current in an RL circuits drops from 1.0 A to 10 mA in the 10 second following removal of the battery from the circuti. If L is 10 H, find the resistance R (in ohm) in the circuit.
View SolutionThe current in a discharging LR circuit without the battery drops from 2.0 A to 0.10 s. (a) find the time constant of the circuit. (b) if the inductance of the circuit is 4.0 H, what is its resistance?
View Solution
Knowledge Check
Power factor of an L-R series circuit is 0.6 and that of a C-R series circuit is 0.5. If the element (L. C, and R) of the two circuits are joined in series the power factor of this circuit is found to be 1. The ratio of the resistance in the L-R circuit to the resistance in the C-R circuit is
A6/5B5/6C43√3D3√34The current from the battery in circuit diagram shown is
 A1AB2AC1.5AD3A
A1AB2AC1.5AD3AThe phase angle between the current and voltage in an L-R circuit is 30∘. What is the impendance of the circuit if the resistance in the circuit is 10√3Ω?
A10ΩB15ΩC20ΩD30Ω
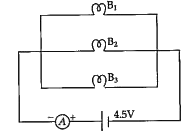
Total current flowing from the battery is 1A. Find the total resistance of the circuit:
View SolutionFind the current supplied by the battery in the following circuit.
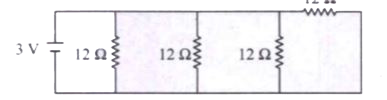
View SolutionDetermine the current supplied by the battery in the circuit as shown
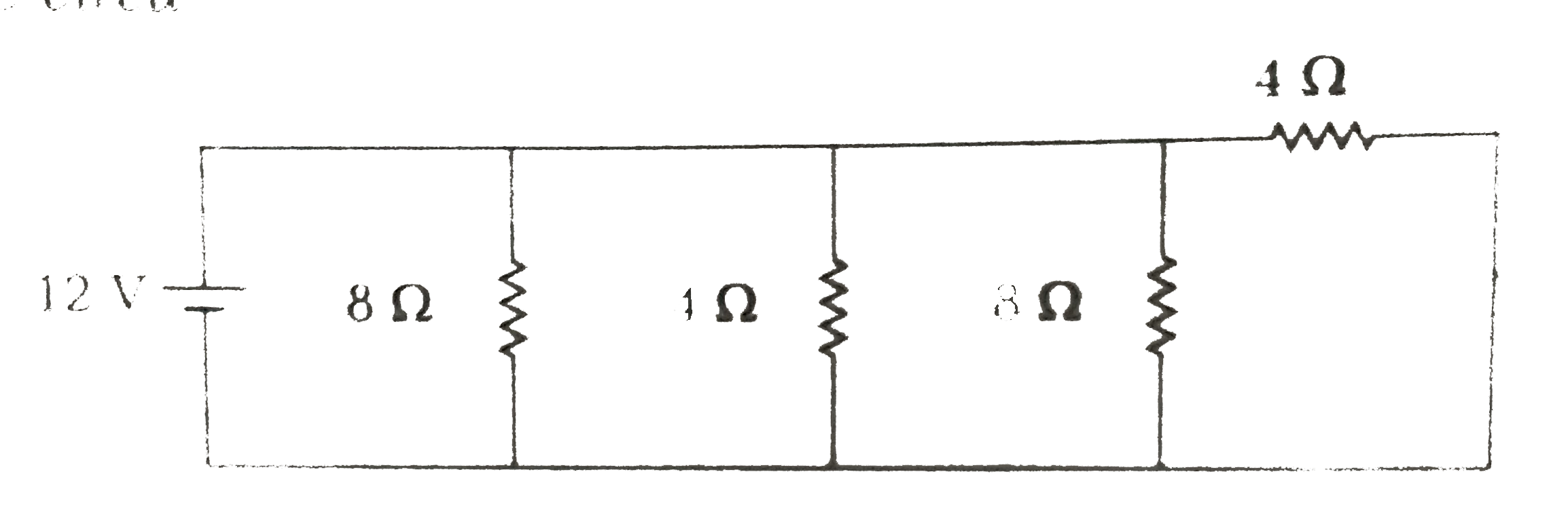
(ii) Find currents in resistance 2Ω and 4Ω.

View SolutionThe power factor of an L-R series circuit is 0.5 and that of a C-R series circuit is 0.2. If the elements (L, C and R) of the two circuit are joined in series and connected to the same ac source, the power factor of this circuit is found to be 1. The ratio of the resistance in the L-R circuit to the resistance in the C-R circuit is
View SolutionThe current in a simple series circuit is 5.0 A. When an additional resistance of 2.0Ω is inserted, the current drops to 4.0 A. The original resistance of the circuit in ohms was
View Solution
