A glass lens is coated on one side with a thin film of magnesium fluoride $(M g F_{2})$ to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of $M g F_{2}$ is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm $(λ = 550 n m)$ ? Assume that the light is approxmately perpendicular to the lens surface.
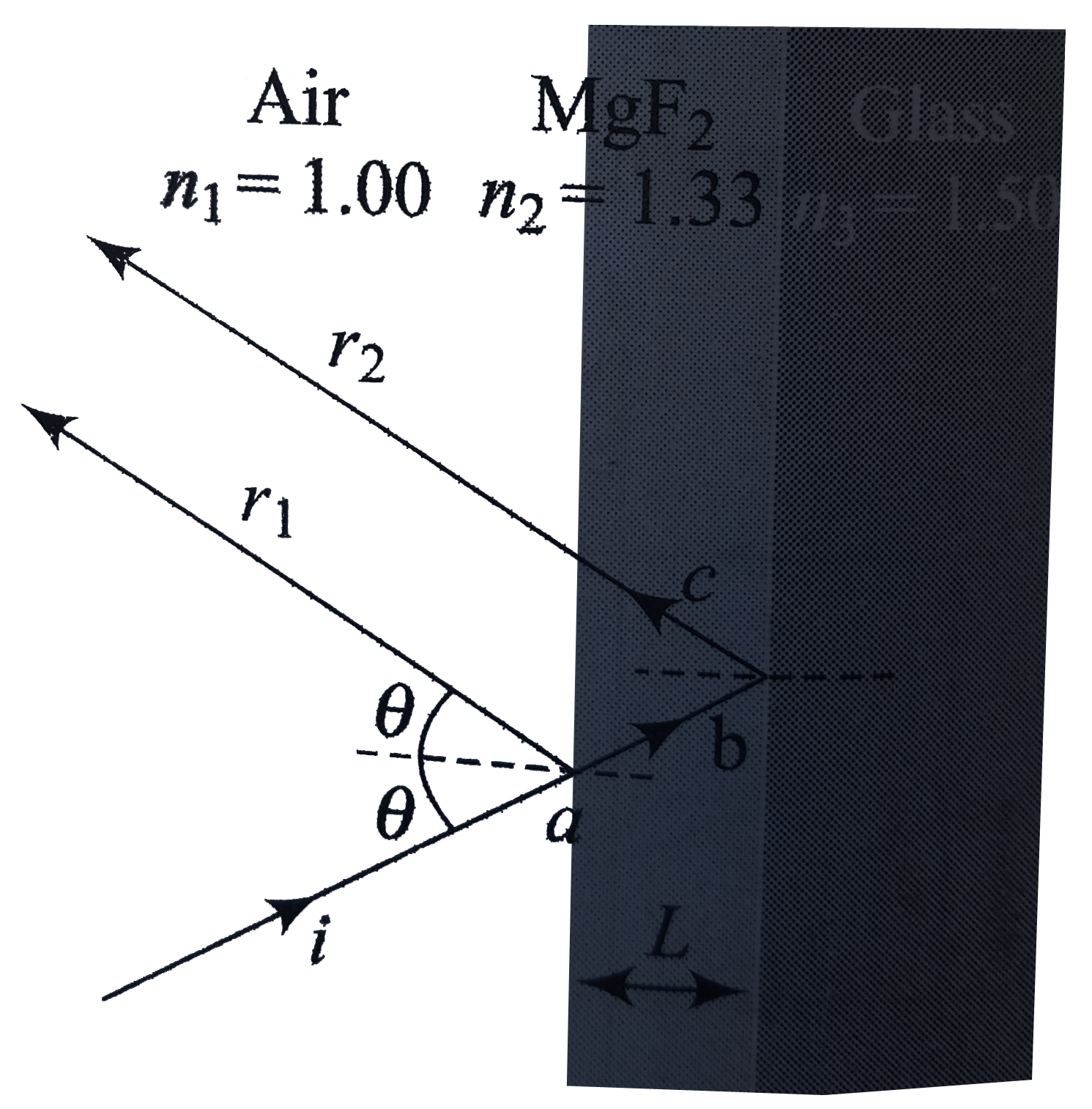
$A glass lens is coated on one side with a thin film of magnesium fluoride (MgF(2))to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF(2) is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (lambda = 550nm)? Assume that the light is approxmately perpendicular to the lens surface.$

Video Solution

Text Solution

Verified by Experts

KEY IDEA
Reflection is eliminated if the film thickness L is such that light waves reflected from the two film interfaces are exactly out of phase. The equation relating L to the given wavelength $λ$ and the index of refraction $n_{2}$ of the thin film is either Eq. 35-50 or Eq. 35-51, depending on the reflection phase shifts at the interfaces.
Calculations: To determine which equation is needed, we fill out an organizing table. At the first interface, the incident light is in air, which has a lesser index of refraction than the $M g F_{2}$ , (the thin film). Thus, we fill in 0.5 wavelength under $r_{1}$ in our organizing table (meaning that the waves of ray $r_{1}$ are shifted by $0.5 λ$ at the first interface). At the second interface, the incident light is in the $M g F_{2}$ , which has a lesser index of refraction than the glass on the other side of the interface. Thus, we fill in 0.5 wavelength under $r_{2}$ in our table.
Because both reflections cause the same phase shift, they tend to put the waves of $r_{1}$ and $r_{2}$ in phase. Since we want those waves to be out of phase, their path length difference 2L must be an odd number of half-wavelengths:
$2 L = \frac{odd number}{2} \times \frac{λ}{n_{2}}$

This leads to Eq. 35-50 (for a bright film sandwiched in air but for a dark film in the arrangement here). Solving that equation for L then gives us the film thicknesses that will eliminate reflection from the lens and coating:
$L = (m + \frac{1}{2}) \frac{λ}{2 n_{2}}$ , for m = 0, 1, 2,.... $(35 - 52)$
We want the least thickness for the coating-that is, the smallest value of L. Thus, we choose m = 0, the smallest possible value of m. Substituting it and the given data in Eq. 35-52, we obtain
$L = \frac{λ}{4 n_{2}} = \frac{550 n m}{(4) (1.38)} = 99.6 n m .$ (Answer)

Updated on:21/07/2023