Suppose that the two waves have wavelength λ=610nm in air. What multiple of λ gives their phase difference when they emerge if (a) n1=1.50,n2=1.60, and L = 700 um, (b) n1=1.62,n2=1.72, and L = 700 um, and (c) n1=1.83,n2=1.59, and L = 2.16 um? (d) Suppose that in each of these three situations the waves arrive at a common point (with the same amplitude) after emerging, Rank the situations according to the brightness the waves produce at the common point.
(a) 1.15, (b) 1.15, (C) 0.85, (d) all tie
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
66 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
23 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
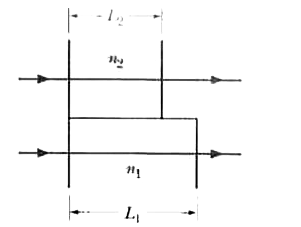
Two waves of light in air, of wavelength λ=600.0nm, are initially in phase. They then both travel through a layer of plastic as shown in Figure, with L1=4.00μm,L2=3.50μm,n1=1.42, and n2=1.60. (a) What multiple of λ gives their phase difference after they both have emerged from the layers? (b) If the waves later arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, interme- diate but closer to fully constructive, or intermediate but closer to fully destructive?
View SolutionUsing the s,p,d notations, describe the orbital with the following quantum numbers :
(a)n=1,l=0 (b)n=3,l=2
(c)n=3,l=1 (d)n=2,l=1
(e)n=4,l=3 (f)n=4,l=2.
View Solution
Knowledge Check
If l1,m1,n1 and l2,m2,n2 are the direction cosines of two lines and l, m, n are the direction cosines of a line perpendicular to the given two lines, then
Al∣∣∣m1n1m2m2∣∣∣=−m∣∣∣l1n1l2n2∣∣∣=n∣∣∣l1n1l2n2∣∣∣Bl∣∣∣m1n1m2m2∣∣∣=−m∣∣∣l1n1l2n2∣∣∣=−n∣∣∣l1n1l2n2∣∣∣C−l∣∣∣m1n1m2m2∣∣∣=−m∣∣∣l1n1l2n2∣∣∣=n∣∣∣l1n1l2n2∣∣∣Dl∣∣∣m1n1m2m2∣∣∣=m∣∣∣l1n1l2n2∣∣∣=n∣∣∣l1n1l2n2∣∣∣Two lines with direction cosines l1,m1,n1andl2,m2,n2 are at right angle of
Al1l2−m1m2−n1n2=0Bl1l2+m1m2+n1n2=0Cl2=l2,m1=m2,n1=n2Dl1l2=m1m2=n1n2
If the direction cosines of two lines are (l1,m1,n1) and
(l2,m2,n2) and the angle between them is θ then
l21+m21+n21=1=l22+m22+n22
and costheta =l1l2+m1m2+n1n2
The angle between the lines whose direction
cosines are (12,12,1√2)and(−12,−12,1√2) isA0∘B60∘C90∘D120∘
The direction cosines of a line satisfy the relations λ(l+m)=nandmn+nl+lm=0. The value of λ, for which the two lines are perpendicular to each other, is a. 1 b. 2 c. 1/2 d. none of these
View SolutionGive the possible value for the missing quantum number (s) in each of the following sets.
(a) n=3,l=0,ml=? , (b) n=3,l=?,ml=−1
(c) n=?,l=1,ml=+1 , (d) n=?,l=2,ml=?.
View SolutionThe three lines through the origin with direction cosines l1,m1,n1,l2,m2,n2, and l3,m3,n3 are coplanar, if
View SolutionSelect the alternatatives.
(a) A diverging beam of light form a point source S having divergence angle α ,falls symmetrically on a glass slab as shown .the angles of incidence of the two extreme rays are equal .Fi the thickness of the glass slab is tand the refractive index nthe n the divergence angle of the emergent beam is (A) zero,(B) α(C)sin−1(1/n)(D)2sin−1(1/n)
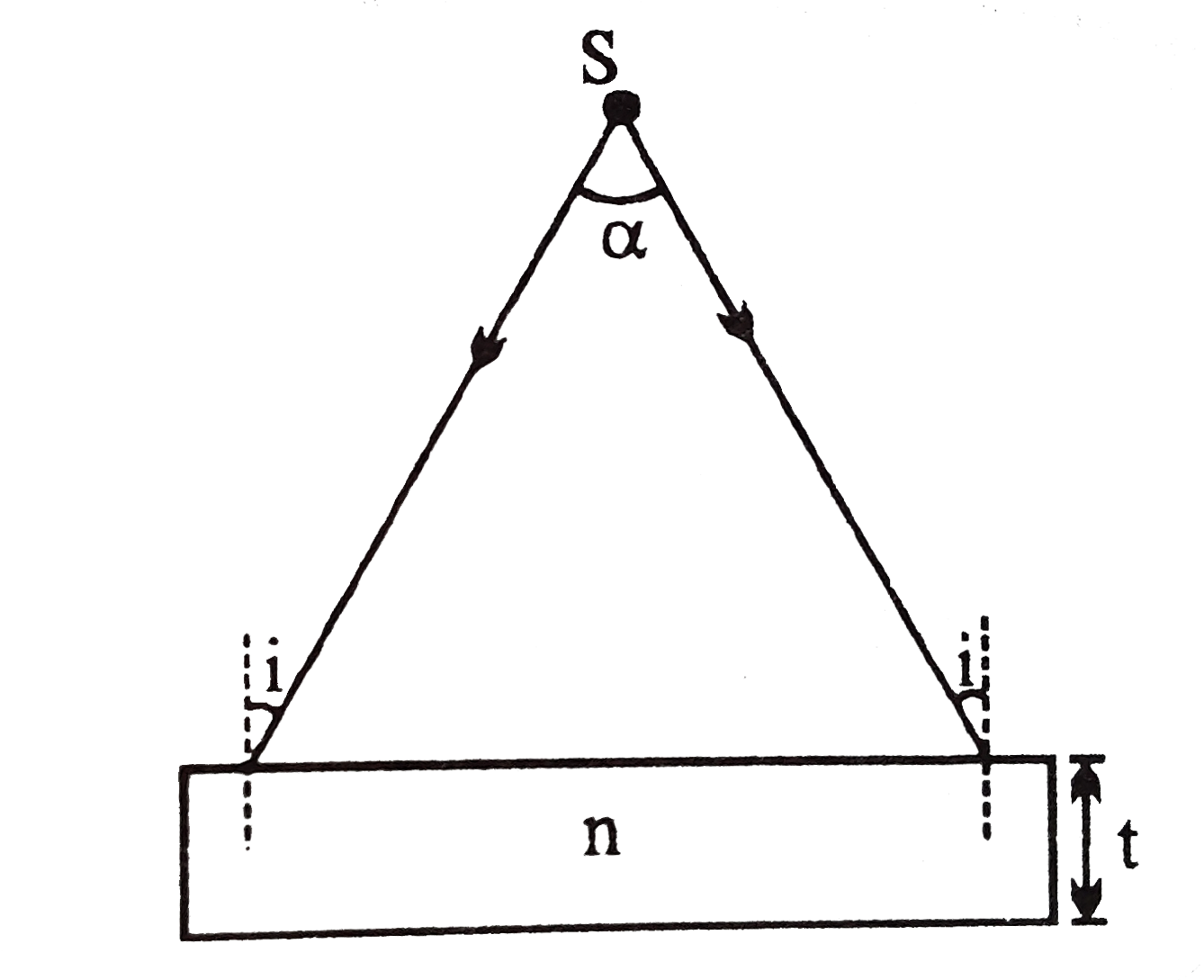
(b) Arectangular glass slab ABCDof refractive index n1 is immersed in water of refractive indexn2(n1>n2) A ray of light is incident at the surface ABof the slab as shown .The maximum value of the angle of incidenc eαmaxsuch that the ray comes out only from the other surface CDis given by
 (A) sin−1[n1n2cos(sin−1n2n1)] (B)sin−1[n1n2cos(sin−11n2)](C)sin−1(n1n2)(D)sin−1(n2n1)
(A) sin−1[n1n2cos(sin−1n2n1)] (B)sin−1[n1n2cos(sin−11n2)](C)sin−1(n1n2)(D)sin−1(n2n1)
(c) A point source of lightB is placed at a distance L inother of the centre of a mirror of width hung vertically ona wall A man walks is front of the mirror along a line parallel to the mirror at a distance 2L from it as shown .the greatest distance over which he can see the image of the light source in the mirror is (A)d/2 (B) d,(c )2d,(d)3d,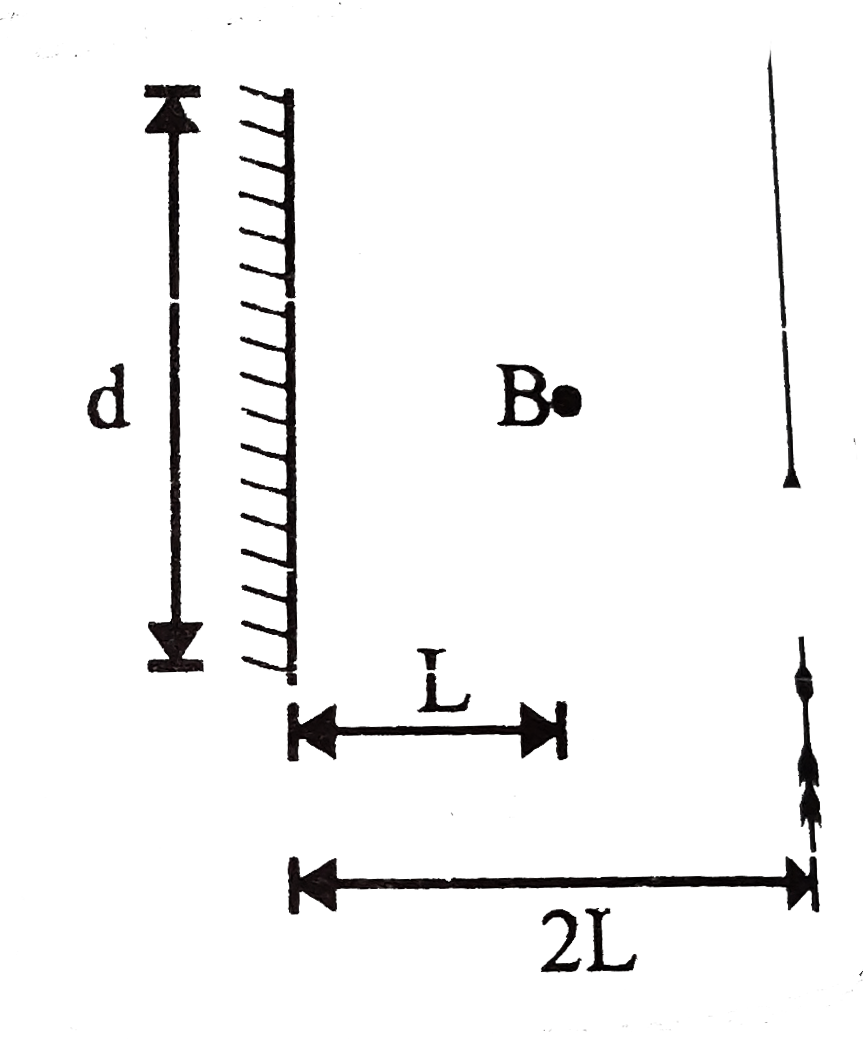 a hollow double concave lens is made of very thin transparents meterial .It can be filled with air or either of two liquids L1andL2having refractive indicesn1andn2respectively(n2>n!>1) the lens will diverge a parallel beam of light of it is filled with (A)air and placed in air.(B) air and immersed inL1(C ),L1 and immersed inL2 (D),L2 ans immersed in L1
a hollow double concave lens is made of very thin transparents meterial .It can be filled with air or either of two liquids L1andL2having refractive indicesn1andn2respectively(n2>n!>1) the lens will diverge a parallel beam of light of it is filled with (A)air and placed in air.(B) air and immersed inL1(C ),L1 and immersed inL2 (D),L2 ans immersed in L1
View SolutionIf θ is the angle between two lines whose d.c's are (l1,m1,n1) and (l2,m2,n2) then the lines are perpendicular if and only if
View Solution
