An unstable high-energy particle enters a detector and leaves a track of length 0.856 mm before it decays. Its speed relative to the detector was 0.992c. What is its proper lifetime? That is, how long would the particle have lasted before decay had it been at rest with respect to the detector?
The correct Answer is:0.446 ps
Topper's Solved these Questions
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Single Corrrect Choice Type)
31 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
11 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - CHECKPOINT
2 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
Similar Questions
A particular particle created in a nuclear reactor leaves a 1cm track before decaying. Assuming that the particle moved at 0.995c , calculate the life of the particle (a) in the lab frame and (b) in the frame of the particle .
View SolutionWhat will be the distance a pion (pi-meson) travels before it decays, if its speed is v - 0.99c and its intrinsic lifetime is to = 2.6×10−8 s? What would be the transit distance if there is no relativistic time dilation? The distance is measured in the laboratory reference frame.
View Solution
Knowledge Check
The proper mean lifetime of a muon is 2.2×10−6s. A beam of muons is moving with speed 0.6c relative to an inertial observer. How far will a muon in the beam travel, on average, before it decays?
A288mB500mC360mD600mWhen subatomic particles undergo reaction energy is conserved, but mass is not necessarily conserved. However, a particle's mass 'contributes' to its total energy, in accordance with Einstein'f famouns equation, E=mc2
In this question, E denotes the equivalent energy when a particle of mass m is converted into energy. The particle can also have additional energy due to its motion and its interactions with other particles.
Consider a neutron at rest, and well separated from other particles. It decays into a proton, an electron, and an undetected third particle: Neutron→proton+electron+third particle
The table below summarizes some data from a single nuetron decay. Column 2 shows the rest mass of the particle times the speed of light squared.
ParticleMxC2Kinetic Energy(MeV)(MeV)Neutron940.970Proton939.660.02Electron0.510.42
Consider an ensemble of particles, all of which have the same positive kinetic energy but different masses. For this ensemble, which graph best represents the relationship between the particle's mass and its total energy ?A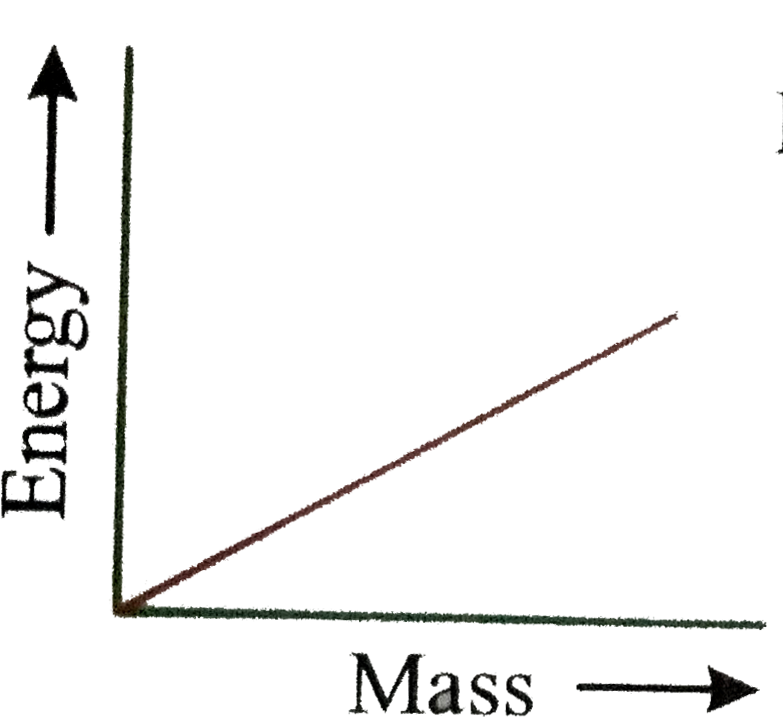 B
B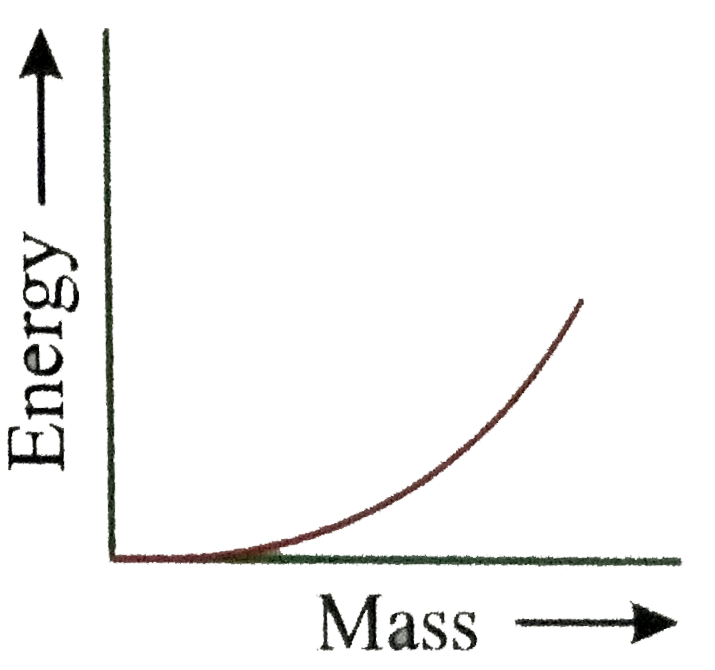 C
C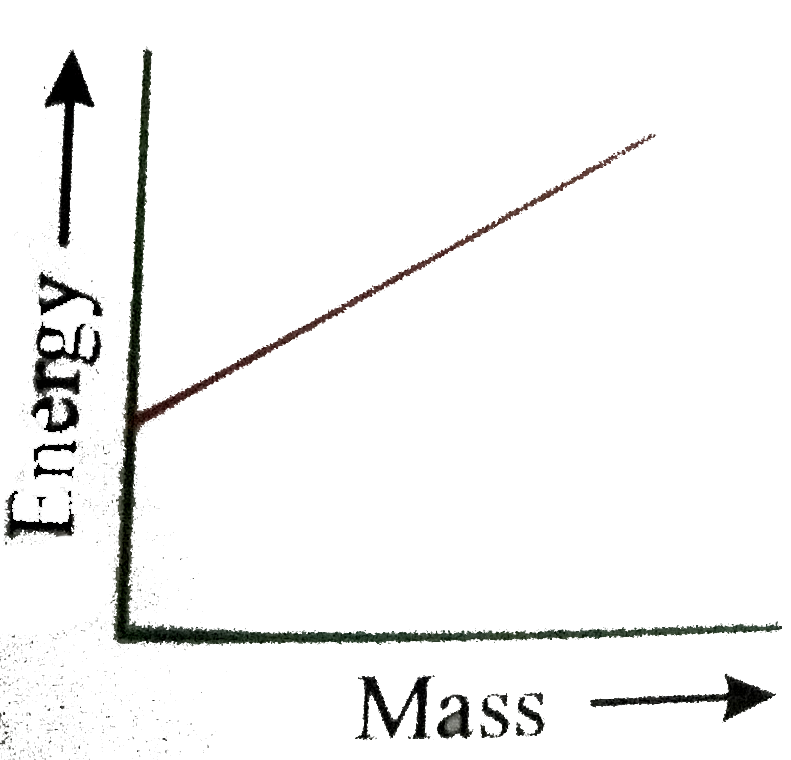 D
D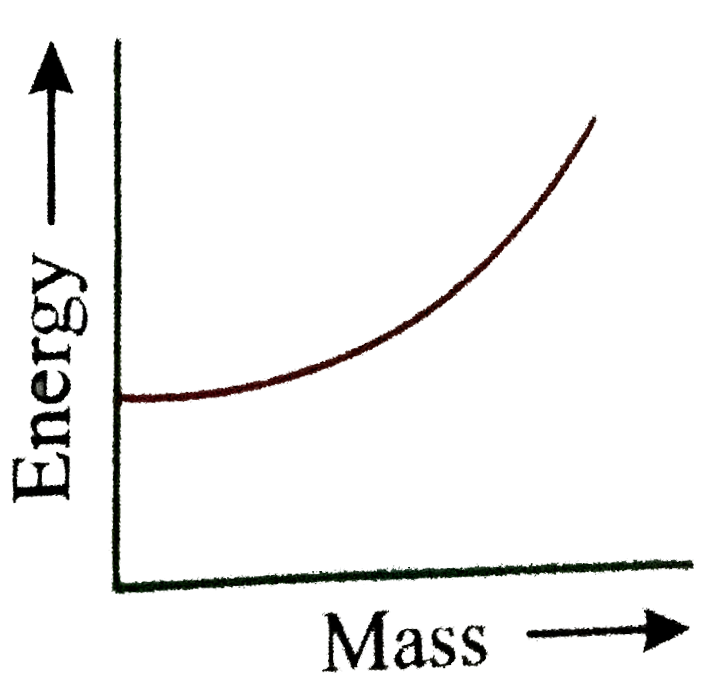
When subatomic particles undergo reaction energy is conserved, but mass is not necessarily conserved. However, a particle's mass 'contributes' to its total energy, in accordance with Einstein'f famouns equation, E=mc2
In this question, E denotes the equivalent energy when a particle of mass m is converted into energy. The particle can also have additional energy due to its motion and its interactions with other particles.
Consider a neutron at rest, and well separated from other particles. It decays into a proton, an electron, and an undetected third particle: Neutron→proton+electron+third particle
The table below summarizes some data from a single nuetron decay. Column 2 shows the rest mass of the particle times the speed of light squared.
ParticleMxC2Kinetic Energy(MeV)(MeV)Neutron940.970Proton939.660.02Electron0.510.42
Assuming the table contains no major errors, what can we conclude about the (mass xc2 of the undetcted third particle ?AIt is 0.90MeVBIt is 0.36MeVCIt is less than or equal to 0.90MeV , but we cannot be more perciseDIt is less than or equal to 0.36MeV , but we cannot be more percise
Two blocks of mass m1=10kg and m2=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. the table is rotating with an angular velocity of 10rad/s. about a vertical axis passing through its center O. the masses are placed along the diameter of the table on either side of the center O such that the mass m1 is at a distance of 0.124m from O. the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m/s2).
(a) Calculate the friction on m1
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on m1.
View SolutionTwo blocks of mass m1=10kg and m2=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. the table is rotating with an angular velocity of 10rad/s. about a vertical axis passing through its center O. the masses are placed along the diameter of the table on either side of the center O such that the mass m1 is at a distance of 0.124m from O. the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m/s2).
(a) Calculate the friction on m1
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on m1.
View SolutionFind the intrinsic lifetime of a particle if its velocity is below the light velocity in vacuum by 0.2% and the distance it travels before decaying is about 300 km.
View SolutionWhen subatomic particles undergo reaction energy is conserved, but mass is not necessarily conserved. However, a particle's mass 'contributes' to its total energy, in accordance with Einstein'f famouns equation, E=mc2
In this question, E denotes the equivalent energy when a particle of mass m is converted into energy. The particle can also have additional energy due to its motion and its interactions with other particles.
Consider a neutron at rest, and well separated from other particles. It decays into a proton, an electron, and an undetected third particle: Neutron→proton+electron+third particle
The table below summarizes some data from a single nuetron decay. Column 2 shows the rest mass of the particle times the speed of light squared.
ParticleMxC2Kinetic Energy(MeV)(MeV)Neutron940.970Proton939.660.02Electron0.510.42
From the given table, which properties of the undetected third particle can we calculate ?
View SolutionWhen subatomic particles undergo reaction energy is conserved, but mass is not necessarily conserved. However, a particle's mass 'contributes' to its total energy, in accordance with Einstein'f famouns equation, E=mc2
In this question, E denotes the equivalent energy when a particle of mass m is converted into energy. The particle can also have additional energy due to its motion and its interactions with other particles.
Consider a neutron at rest, and well separated from other particles. It decays into a proton, an electron, and an undetected third particle: Neutron→proton+electron+third particle
The table below summarizes some data from a single nuetron decay. Column 2 shows the rest mass of the particle times the speed of light squared.
ParticleMxC2Kinetic Energy(MeV)(MeV)Neutron940.970Proton939.660.02Electron0.510.42
Could this reaction occur ?
Proton→neutron+other particles
View Solution
