When subatomic particles undergo reaction energy is conserved, but mass is not necessarily conserved. However, a particle's mass 'contributes' to its total energy, in accordance with Einstein'f famouns equation, E=mc2
In this question, E denotes the equivalent energy when a particle of mass m is converted into energy. The particle can also have additional energy due to its motion and its interactions with other particles.
Consider a neutron at rest, and well separated from other particles. It decays into a proton, an electron, and an undetected third particle: Neutron→proton+electron+third particle
The table below summarizes some data from a single nuetron decay. Column 2 shows the rest mass of the particle times the speed of light squared.
ParticleMxC2Kinetic Energy(MeV)(MeV)Neutron940.970Proton939.660.02Electron0.510.42
Could this reaction occur ?
Proton→neutron+other particles
Yes, if the other particles have much more kinetic energy than mass energy
Yes, but only if the proton has potential energy (due to interactions with other particles)
No, because a neutron is more massive than a proton
No, because a proton is positively charged while a neutron is electrically neutral
The correct Answer is:B
A proton with only mass-energy can never decay into a neutron as the mass of neutro is more than that of the proton. However, If the proton has some additional energy in the form of PE such that its energy is more than rest mass-energy of the neutron, it can decay into neutron and release some energy.
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - Previous JEE questions
21 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-I-(H.W)
16 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - Level-V Multiple answer questions
45 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 4
20 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
Similar Questions
Knowledge Check
When subatomic particles undergo reaction energy is conserved, but mass is not necessarily conserved. However, a particle's mass 'contributes' to its total energy, in accordance with Einstein'f famouns equation, E=mc2
In this question, E denotes the equivalent energy when a particle of mass m is converted into energy. The particle can also have additional energy due to its motion and its interactions with other particles.
Consider a neutron at rest, and well separated from other particles. It decays into a proton, an electron, and an undetected third particle: Neutron→proton+electron+third particle
The table below summarizes some data from a single nuetron decay. Column 2 shows the rest mass of the particle times the speed of light squared.
ParticleMxC2Kinetic Energy(MeV)(MeV)Neutron940.970Proton939.660.02Electron0.510.42
Consider an ensemble of particles, all of which have the same positive kinetic energy but different masses. For this ensemble, which graph best represents the relationship between the particle's mass and its total energy ?A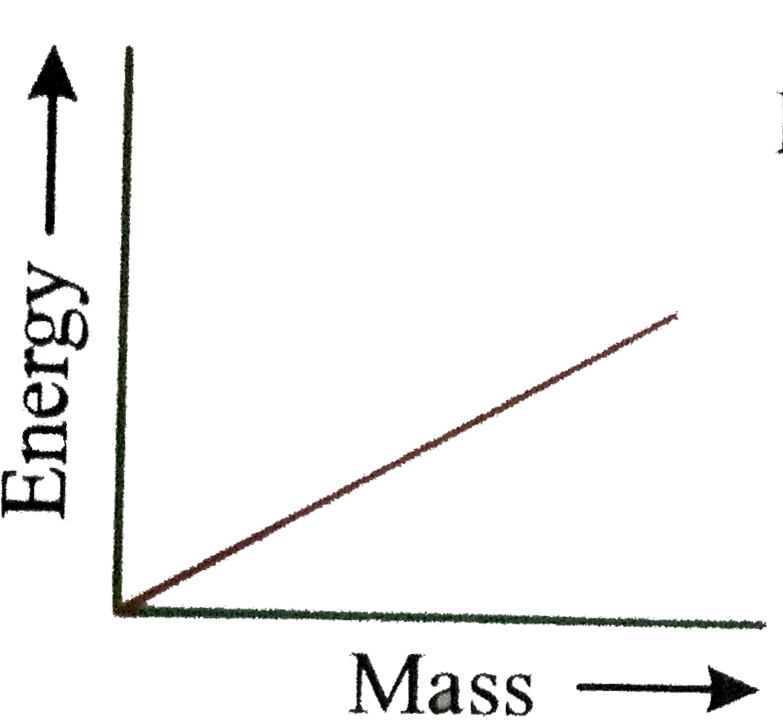 B
B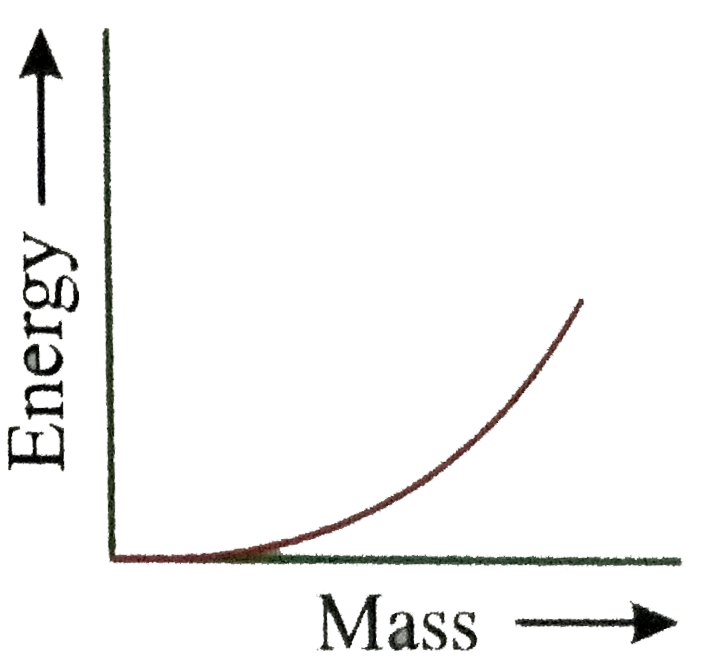 C
C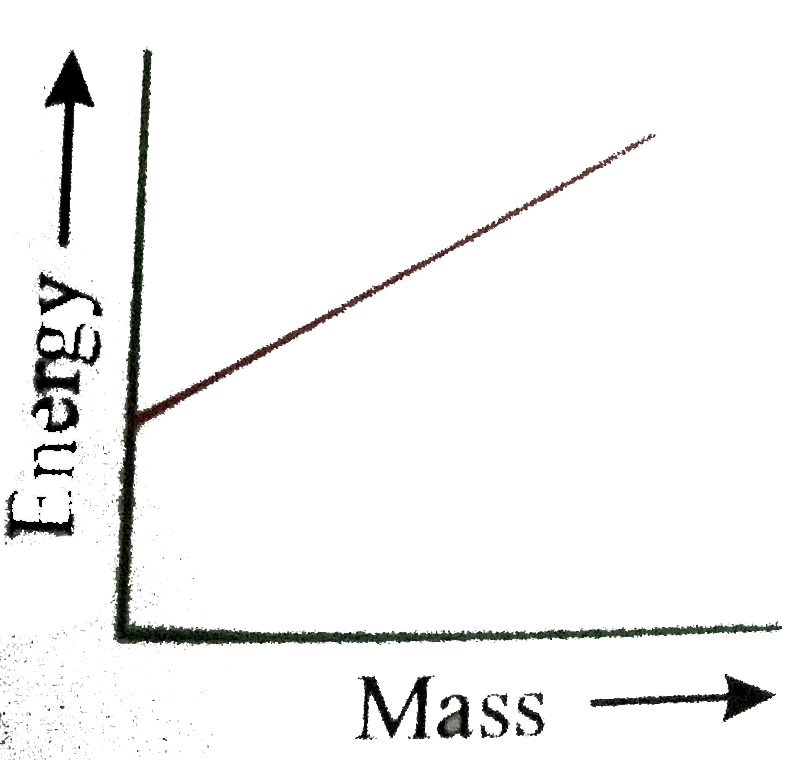 D
D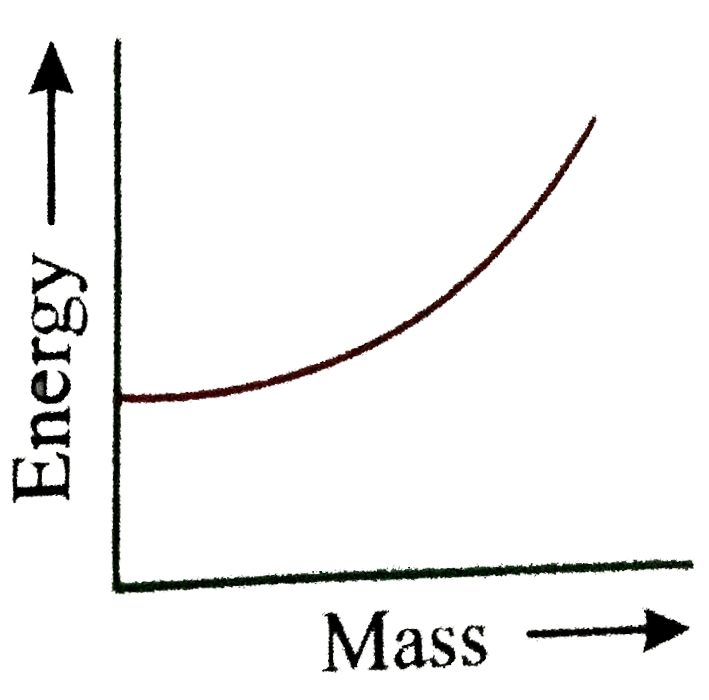
When subatomic particles undergo reaction energy is conserved, but mass is not necessarily conserved. However, a particle's mass 'contributes' to its total energy, in accordance with Einstein'f famouns equation, E=mc2
In this question, E denotes the equivalent energy when a particle of mass m is converted into energy. The particle can also have additional energy due to its motion and its interactions with other particles.
Consider a neutron at rest, and well separated from other particles. It decays into a proton, an electron, and an undetected third particle: Neutron→proton+electron+third particle
The table below summarizes some data from a single nuetron decay. Column 2 shows the rest mass of the particle times the speed of light squared.
ParticleMxC2Kinetic Energy(MeV)(MeV)Neutron940.970Proton939.660.02Electron0.510.42
Assuming the table contains no major errors, what can we conclude about the (mass xc2 of the undetcted third particle ?AIt is 0.90MeVBIt is 0.36MeVCIt is less than or equal to 0.90MeV , but we cannot be more perciseDIt is less than or equal to 0.36MeV , but we cannot be more perciseWhen subatomic particles undergo reaction energy is conserved, but mass is not necessarily conserved. However, a particle's mass 'contributes' to its total energy, in accordance with Einstein'f famouns equation, E=mc2
In this question, E denotes the equivalent energy when a particle of mass m is converted into energy. The particle can also have additional energy due to its motion and its interactions with other particles.
Consider a neutron at rest, and well separated from other particles. It decays into a proton, an electron, and an undetected third particle: Neutron→proton+electron+third particle
The table below summarizes some data from a single nuetron decay. Column 2 shows the rest mass of the particle times the speed of light squared.
ParticleMxC2Kinetic Energy(MeV)(MeV)Neutron940.970Proton939.660.02Electron0.510.42
From the given table, which properties of the undetected third particle can we calculate ?ATotal energy but not kinetic energyBKinetic energy, but not total energyCBoth total energy, but not kinetic energyDNeither total energy nor kinetic energy
A particle of mass m is executing SHM about its mean position. The total energy of the particle at given instant is
View SolutionIf 'p' be the linear momentum of a particle of mass 'm', then its kinetic energy will be
View SolutionA particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
View SolutionA particle of mass m executing S.H.M. about its mean position. The total energy of the particle at given instant is
View SolutionA particle of mass m is projected at an angle with horizontal with kinetic energy E. the potential energy at the top of its trajectory is E2. Find the range.
View Solution
