A yo-yo has mass M = 0.550 kg and rotational inertia I=3.40×10−4kgm2?. It rolls from rest down a string of length L = 17.0 cm. What is its angular speed at the bottom?
The mechanical energy of the yo-yo is conserved during the descent.
Calculations: Let the bottom position be the reference level for zero gravitational potential energy. Then at the initial point (at height y = L) the mechanical energy is
Ei=Ki+Ui=0+MgL.
The symbol Ki is the sum of the translational kinetic energy and rotational kinetic energy, both of which are zero. At the bottom (at height y= 0), the translational kinetic energy and gravitational potential energy are zero. So, the mechanical energy is just the rotational kinetic energy 1/2Iω2 and we have
Ef=Kf+Uf=12Iω2
Because the mechanical energy does not change, Ef=Ei
12Iω2=MgL
Solving for omega and substituting the given values lead to
ω=73.4rad/s
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - EXAMPLE1videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
A yo-yo has mass M 0.550 kg, axle radius R0=3.2mm, and rotational inertia l=3.4×10−4kgm2 about its rotation axis. Assume that the string has negligible mass and thickness.
(a) What is the linear acceleration of the yo-yo as it rolls down the string from rest?View SolutionA yo-yo has mass M 0.550 kg, axle radius R0=3.2mm, and rotational inertia l=3.4×10−4kgm2 about its rotation axis. Assume that the string has negligible mass and thickness.
What is the tension in the string as the yo-yo descends?View Solution
Knowledge Check
- Question 1 - Select One
A block mass 3 kg slides down a frictionless inclined plane of length 6 m and height 4 m. if the block is released from rest at the top of the incline, what is its speed at the bottom?
A5m/sB6m/sC8m/sD9m/s - Question 2 - Select One
A horizontal platform in the shape of a circular disk rotates on a frictionless bearing about a vertical axle through the centre of the disk. The platform has a mass of 150kg, a radius of 2.0m, and a rotational inertia of300kgm2 about the axis of rotation. A 60kg student walks slowly from the rim of the platform toward the centre. If the angular speed of the system is 1.5rad/s when the student starts at the rim, what is the angular speed when she is 0.50m from the centre ?
A1.2rad/sB2.6rad/sC1.5rad/sD3.6rad/s - Question 3 - Select One
A torque of 30 N-m is acting on a wheel of mass 5 kg and moment of inertia 2kg−m2. If wheel starts rotating from rest then its angular displacement in 10 seconds will be-
A750radB1500radC300radD6000rad
A uniform spherical shell of mass M = 4.5 kg and radius R = 8.5 cm can rotate about a vertical axis on frictionless bearings (Fig. 10-69). A massless cord passes around the equator of the shell, over a pulley of rotational inertia I=3.0×10−3kg⋅m2 and radius r = 5.0 cm, and is attached to a small object of mass m = 0.60 kg. There is no friction on the pulley's axle, the cord does not slip on the pulley. What is the speed of the object when it has fallen 82 cm after being released from rest? Use energy considerations.
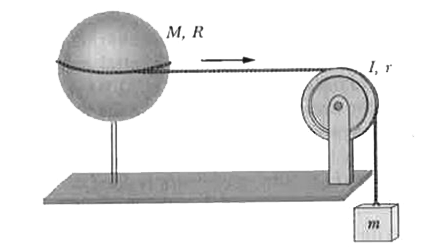 View Solution
View SolutionA uniform ball, of mass M = 6.00 kg and radius R, rolls smoothly from rest down a ramp at angle θ=30.0∘ .
(a) The ball descends a vertical height h = 1.20 m to reach the bottom of the ramp. What is its speed at the bottom?View SolutionA yo-yo has a rotational inertia of 950gcm2 and a mass of 120 g. Its axle radius is 3.2 mm, and its string is 120 cm long. The yo-yo rolls from rest down to the end of the string. (a) What is the magnitude of its linear acceleration? (b) How long does it take to reach the end of the string? As it reaches the end of the string, what are its (c) linear speed, (d) translational kinetic energy, (e) rotational kinetic energy, and (f) angular speed?
View SolutionThe uniform rod (length 0.60 m, mass 1.0 kg) in Fig. 10-85 rotates in the plane of the figure about an axis through one end, with a rotational inertia of 0.12kg⋅m2. As the rod swings through its lowest position, it collides with a 0.20 kg putty wad that sticks to the end of the rod. If the rod's angular speed just before collision is 2.4 rad/s, what is the angular speed of the rod-putty system immediately after collision?
 View Solution
View SolutionA pulley, with a rotational inertia of 1.0×10−3kg⋅m2 about its axle and a radius of 10 cm, is acted on by a force applied tangentially at its rim. The force magnitude varies in time as F=0.50t+0.30t2, with F in newtons and t in seconds. The pulley is initially at rest. At t = 3.0 s what are its (a) angular acceleration and (b) angular speed?
View Solution

