A yo-yo has mass M 0.550 kg, axle radius R0=3.2mm, and rotational inertia l=3.4×10−4kgm2 about its rotation axis. Assume that the string has negligible mass and thickness.
(a) What is the linear acceleration of the yo-yo as it rolls down the string from rest?
To find the linear acceleration of the yo-yo as it rolls down the string from rest, we can follow these steps:
Step 1: Identify the forces acting on the yo-yo
The forces acting on the yo-yo are:
- The gravitational force (weight) acting downward: Fg=Mg
- The tension in the string acting upward: T
Step 2: Write the equation of motion
Using Newton's second law, we can write the equation for the linear motion of the yo-yo:
Mg−T=Ma(1)
where:
- M is the mass of the yo-yo (0.550 kg),
- g is the acceleration due to gravity (approximately 9.8 m/s²),
- a is the linear acceleration of the yo-yo.
Step 3: Write the torque equation
The yo-yo also rotates as it falls, so we need to consider the torque about its axis of rotation. The torque τ due to the tension in the string is given by:
τ=TR=Iα(2)
where:
- R is the radius of the axle (3.2 mm = 0.0032 m),
- I is the moment of inertia of the yo-yo (3.4 × 10^(-4) kg m²),
- α is the angular acceleration.
Step 4: Relate linear acceleration and angular acceleration
The relationship between linear acceleration a and angular acceleration α is given by:
a=Rα(3)
From this, we can express α in terms of a:
α=aR(4)
Step 5: Substitute α into the torque equation
Substituting equation (4) into equation (2):
TR=I(aR)
Rearranging gives:
T=IaR2(5)
Step 6: Substitute T back into the equation of motion
Now substitute equation (5) into equation (1):
Mg−IaR2=Ma
Rearranging gives:
Mg=Ma+IaR2
Factoring out a:
Mg=a(M+IR2)
Step 7: Solve for linear acceleration a
Now we can solve for a:
a=MgM+IR2(6)
Step 8: Plug in the values
Now substituting the known values:
- M=0.550kg
- g=9.8m/s2
- I=3.4×10−4kg m2
- R=3.2×10−3m
Calculating IR2:
IR2=3.4×10−4(3.2×10−3)2=3.4×10−41.024×10−5≈33.2kg
Now substituting into equation (6):
a=0.550×9.80.550+33.2≈5.3933.75≈0.160m/s2
Final Answer
The linear acceleration of the yo-yo as it rolls down the string from rest is approximately 0.160m/s2.
---
The forces acting on the yo-yo are:
- The gravitational force (weight) acting downward: Fg=Mg
- The tension in the string acting upward: T
Using Newton's second law, we can write the equation for the linear motion of the yo-yo:
Mg−T=Ma(1)
where:
- M is the mass of the yo-yo (0.550 kg),
- g is the acceleration due to gravity (approximately 9.8 m/s²),
- a is the linear acceleration of the yo-yo.
The yo-yo also rotates as it falls, so we need to consider the torque about its axis of rotation. The torque τ due to the tension in the string is given by:
τ=TR=Iα(2)
where:
- R is the radius of the axle (3.2 mm = 0.0032 m),
- I is the moment of inertia of the yo-yo (3.4 × 10^(-4) kg m²),
- α is the angular acceleration.
The relationship between linear acceleration a and angular acceleration α is given by:
a=Rα(3)
From this, we can express α in terms of a:
α=aR(4)
Substituting equation (4) into equation (2):
TR=I(aR)
Rearranging gives:
T=IaR2(5)
Now substitute equation (5) into equation (1):
Mg−IaR2=Ma
Rearranging gives:
Mg=Ma+IaR2
Factoring out a:
Mg=a(M+IR2)
Now we can solve for a:
a=MgM+IR2(6)
Now substituting the known values:
- M=0.550kg
- g=9.8m/s2
- I=3.4×10−4kg m2
- R=3.2×10−3m
IR2=3.4×10−4(3.2×10−3)2=3.4×10−41.024×10−5≈33.2kg
a=0.550×9.80.550+33.2≈5.3933.75≈0.160m/s2
The linear acceleration of the yo-yo as it rolls down the string from rest is approximately 0.160m/s2.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - EXAMPLE1videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
A yo-yo has mass M 0.550 kg, axle radius R0=3.2mm, and rotational inertia l=3.4×10−4kgm2 about its rotation axis. Assume that the string has negligible mass and thickness.
What is the tension in the string as the yo-yo descends?View SolutionA yo-yo has mass M = 0.550 kg and rotational inertia I=3.40×10−4kgm2?. It rolls from rest down a string of length L = 17.0 cm. What is its angular speed at the bottom?
View Solution
Knowledge Check
- Question 1 - Select One
A horizontal platform in the shape of a circular disk rotates on a frictionless bearing about a vertical axle through the centre of the disk. The platform has a mass of 150kg, a radius of 2.0m, and a rotational inertia of300kgm2 about the axis of rotation. A 60kg student walks slowly from the rim of the platform toward the centre. If the angular speed of the system is 1.5rad/s when the student starts at the rim, what is the angular speed when she is 0.50m from the centre ?
A1.2rad/sB2.6rad/sC1.5rad/sD3.6rad/s - Question 2 - Select One
A solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg-m2) about its geometrical axis is :
A0.8kg-m2B0.4kg-m2C0.2 kg-m2D20.2 kg-m2 - Question 3 - Select One
A solid cylinder of mass 20 kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg m ) about its geometrical axis is (in kg m2)
A0.8B0.4C0.2D0.6
The pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
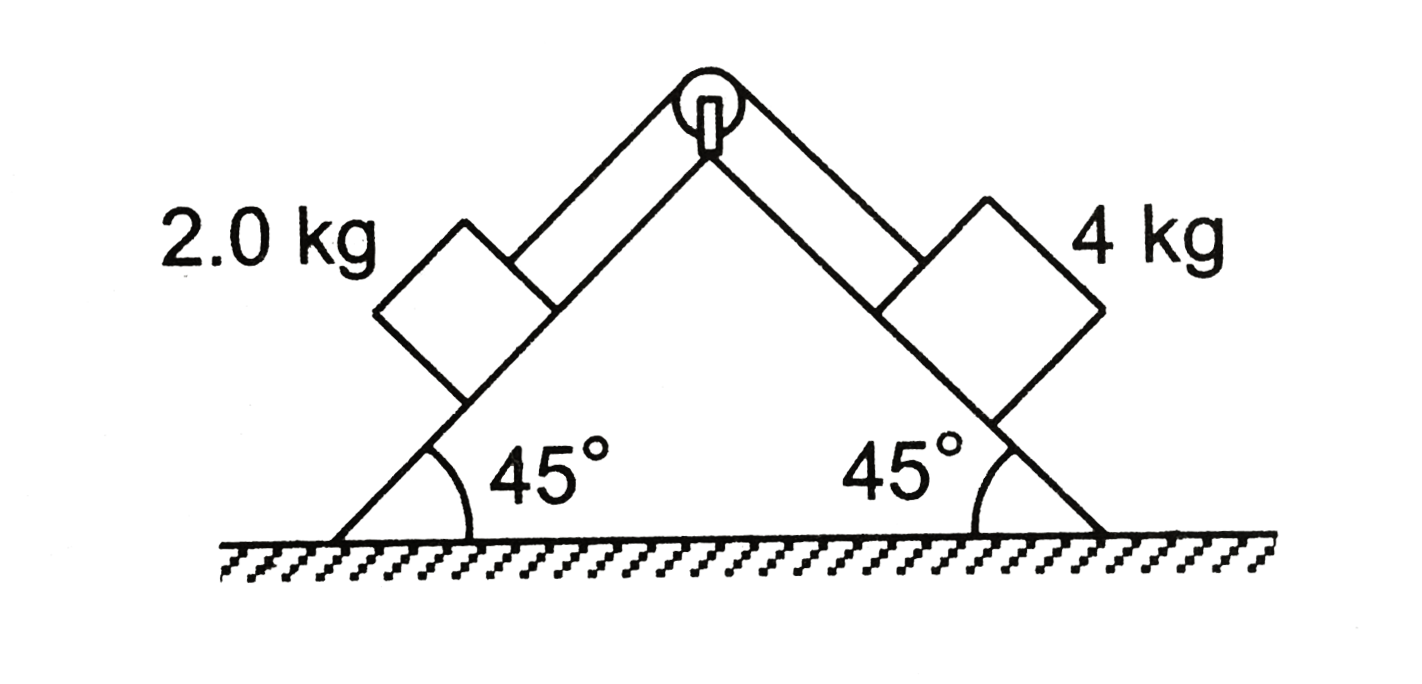 View Solution
View SolutionA yo-yo has a rotational inertia of 950gcm2 and a mass of 120 g. Its axle radius is 3.2 mm, and its string is 120 cm long. The yo-yo rolls from rest down to the end of the string. (a) What is the magnitude of its linear acceleration? (b) How long does it take to reach the end of the string? As it reaches the end of the string, what are its (c) linear speed, (d) translational kinetic energy, (e) rotational kinetic energy, and (f) angular speed?
View SolutionThe rotor of an electric motor has rotational inertia Im=2.0×10−3kg⋅m2 about its central axis. The motor is used to change the orientation of the space probe in which it is mounted. The motor axis is mounted along the central axis of the probe, the probe has rotational inertia Ip=10kg⋅m2 about this axis. Calculate the number of revolutions of the rotor required to turn the probe through 30∘ about its central axis.
View SolutionA top spins at 25 rev/s about an axis that makes an angle of 30∘ with the vertical. The mass of the top is 0.50 kg, its rotational inertia about its central axis is 5.0×10−4kg⋅m2, and its center of mass is 4.2 cm from the pivot point. If the spin is clockwise from an overhead view, what are the (a) precession rate and (b) direction of the precession as viewed from overhead?
View SolutionA wheel of mass 10 kg has a moment of inertia of 160kg−m2 about its own axis, the radius of gyration will be
View Solution

