In Fig. the driver of a car on a horizontal road makes an emergency stop by applying the brakes so that all four wheels lock and skid along the road. The coefficient of kinetic friction between tires and road is 0.37. The separation between the front and rear axles is L = 4.0 m, and the center of mass of the car is located at distance d = 1.9 m behind the front axle and distance h=0.75 m above the road. The car weighs 11 kN. Find the magnitude of (a) the braking acceleration of the car, (b) the normal force on each rear wheel, (c) the normal force on each front wheel, (d) the braking force on each rear wheel, and (e) the braking force on each front wheel. (Hint: Although the car is not in translational equilibrium, it is in rotational equilibrium.)
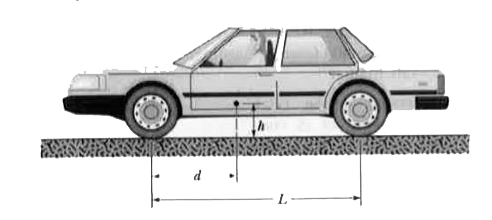
(a) 3.63m/s2 , (b) 2.2×103N, (c) 3.3×103 N, (d)8.1×102 N, (e) 1.2×103N
Topper's Solved these Questions
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS
28 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)
2 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
Similar Questions
What is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is μ.
View SolutionThe stopping distance for a vehicle of mass M moving with a speed v along a level road, will be - (µ is the coefficient of friction between tyres and the road)
View Solution
Knowledge Check
What is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is μ.
Av22μgB2v2μgCv2μgDNone of theseWhat is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is μ
Av22μgB2v2μgCv2μgDnone of theseIf μ is the coefficient of friction between the tyres and road then the least stopping distance for a car of mass m moving with velocity v is
Av2/2μgBv/2μgC2v/μ2gD2v/μg
A car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tire and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionA car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyres and the road is μ , the shortest distance in which the car can be stopped is
View SolutionConsider a car moving along a straight horizontal road with a speed of 72 km / h . If the coefficient of kinetic friction between the tyres and the road is 0.5, the shortest distance in which the car can be stopped is [g=10ms−2]
View SolutionA car is travelling along a curved road of radius r. If the coefficient of friction between the tyres and the road is μ the car will skid if its speed exceeds .
View SolutionConsider a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between road and tyres is 0.5, the shortest distance in which the car can be stopped is
View Solution
