Doubtnut Promotions Sticky

A paricle starting from the origin (0,0) moves in a straight line in (x,y) plane. Its coordinates at a later time are (√3,3). The path of the particle makes with the x-axis an angle of

A

45∘

B

60∘

C

0∘

D

30∘

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:b

tanθ=3√3=√3
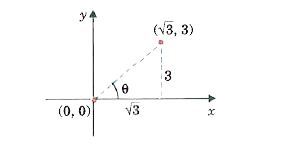
ocr_image
θ=60∘

|
Updated on:21/07/2023
Class 11PHYSICSRECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    A particle starting from the origin (0,0) moves in a straight line in the (x,y) plane. Its coordinates at a later time are (√3,3). The path of the particle makes with the x-axis an angle of

    A30∘
    B45∘
    C60∘
    D0∘
  • Question 2 - Select One

    A particle starting from the origin (0,0) moves in a straight line in the (x,y) plane. Its coordinates at a later time are (√3,3). The path of the particle makes with the x-axis an angle of

    A30∘
    B45∘
    C60∘
    D0∘
  • Question 3 - Select One

    A paricle starting from the origin (0,0) moves in a straight line in (x,y) plane. Its coordinates at a later time are (√3,3). The path of the particle makes with the x-axis an angle of

    A45∘
    B60∘
    C0∘
    D30∘