A particle moves along the straight line y=3x+5. Which coordinate changes at a faster rate ?
x- coordinate
y- coordinate
Both x and y coordinates
Data insufficient
The correct Answer is:2
To determine which coordinate changes at a faster rate for a particle moving along the straight line given by the equation y=3x+5, we can follow these steps:
Step 1: Understand the relationship between x and y
The equation y=3x+5 shows that y is a linear function of x. The slope of the line is 3, which indicates how y changes with respect to x.
Step 2: Differentiate the equation with respect to time
To find how the coordinates change with respect to time, we differentiate both sides of the equation with respect to time t:
dydt=ddt(3x+5)
Step 3: Apply the chain rule
Using the chain rule, we differentiate the right-hand side:
dydt=3dxdt+0
The derivative of the constant (5) is zero.
Step 4: Simplify the equation
This simplifies to:
dydt=3dxdt
Step 5: Compare the rates of change
From the equation dydt=3dxdt, we can see that the rate of change of y with respect to time is three times the rate of change of x with respect to time. This indicates that y changes at a faster rate than x.
Conclusion
Thus, the y-coordinate changes at a faster rate than the x-coordinate.
Final Answer
The y-coordinate changes at a faster rate.
---
The equation y=3x+5 shows that y is a linear function of x. The slope of the line is 3, which indicates how y changes with respect to x.
To find how the coordinates change with respect to time, we differentiate both sides of the equation with respect to time t:
Using the chain rule, we differentiate the right-hand side:
This simplifies to:
From the equation dydt=3dxdt, we can see that the rate of change of y with respect to time is three times the rate of change of x with respect to time. This indicates that y changes at a faster rate than x.
Thus, the y-coordinate changes at a faster rate than the x-coordinate.
The y-coordinate changes at a faster rate.
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - GEOMETRY
7 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - DEFINITION & TYPES OF VECTOR
6 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - BEGINNER S BOX 12
4 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
Similar Questions
Knowledge Check
A particle moves along the straight line y=3x+5. Which coordinate changes at faster rate?
Ax-coordinateBy-coordinateCBoth x and y coordinateDData insufficient.A particle is moving along a straight line.
AIf the acceleration of the particle is more than that of another object, the particle is moving faster.BIf the acceleration is positive, the speed must be increasing.CIf the acceleration and the velocity have the same sign, the speed must be increasing.DIf the acceleration is zero, the velocity is constant but the speed may be changing.A particle moves along the curve 12y=x3. . Which coordinate changes at faster rate at x=10?
Ax-coordinateBy-coordinateCBoth x and y-coordinateDData insufficient
If a particle is moving along straight line with increasing speed, then
View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line
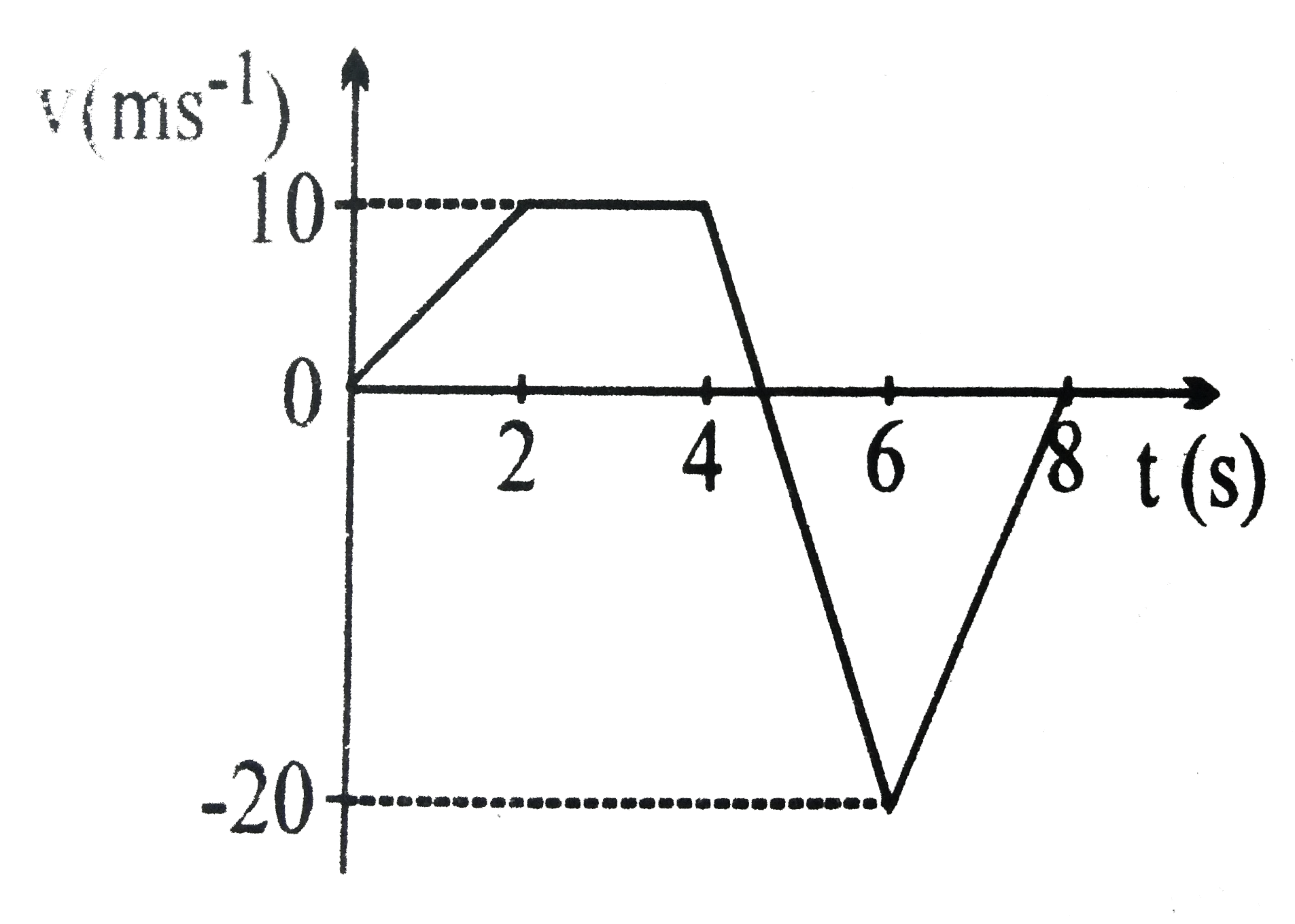
Identify the region in which the rate of change of velocity ∣∣∣Δ→vΔt∣∣∣ of the particle is maximum
View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line

Identify the region in which the rate of change of velocity ∣∣∣Δ¯vΔt∣∣∣ of the particle is maximum
View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line
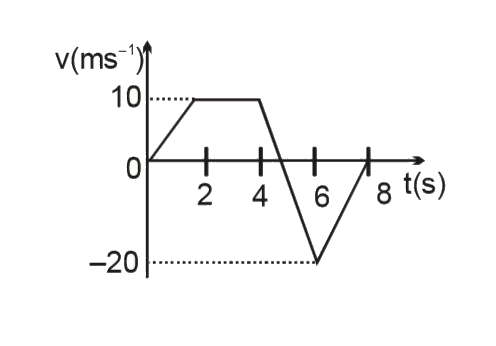
Q. Identify the region in which the rate of change of velocity ∣∣∣Δ→vΔt∣∣∣ of the particle is maximum
View SolutionConsider the parabola y=x2+7x+2 and the straight line y = 3x -3.
What are the coordinates of the point on the parabola which is closest to the straight line?
View Solution
