A particle is moving in a straight line. All the physical quantities are to be measured in MKS system. Square of the magnitude of its instantaneous velocity is found to be ten times its instantaneous displacement . What is the acceleration of the particle?
The correct Answer is:5
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the given information
We are given that the square of the magnitude of the instantaneous velocity (v²) is equal to ten times the instantaneous displacement (s). Mathematically, this can be expressed as:
v2=10s
Step 2: Identify the relevant equations
In the case of uniform acceleration, we can use the kinematic equation that relates velocity, displacement, and acceleration:
v2=u2+2as
where:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = displacement
Step 3: Set initial conditions
Since the problem does not mention any initial velocity, we can assume that the particle starts from rest. Therefore:
u=0
Step 4: Substitute into the kinematic equation
Substituting u=0 into the kinematic equation gives:
v2=0+2as
or simply:
v2=2as
Step 5: Equate the two expressions for v²
From Step 1, we have v2=10s. From Step 4, we have v2=2as. Setting these two equations equal to each other:
10s=2as
Step 6: Simplify the equation
We can divide both sides by s (assuming s≠0):
10=2a
Step 7: Solve for acceleration (a)
Now, we can solve for a:
a=102=5m/s2
Conclusion
The acceleration of the particle is 5m/s2.
---
We are given that the square of the magnitude of the instantaneous velocity (v²) is equal to ten times the instantaneous displacement (s). Mathematically, this can be expressed as:
v2=10s
In the case of uniform acceleration, we can use the kinematic equation that relates velocity, displacement, and acceleration:
v2=u2+2as
where:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = displacement
Since the problem does not mention any initial velocity, we can assume that the particle starts from rest. Therefore:
u=0
Substituting u=0 into the kinematic equation gives:
v2=0+2as
or simply:
v2=2as
From Step 1, we have v2=10s. From Step 4, we have v2=2as. Setting these two equations equal to each other:
10s=2as
We can divide both sides by s (assuming s≠0):
10=2a
Now, we can solve for a:
a=102=5m/s2
The acceleration of the particle is 5m/s2.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS )1videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)12videos
OSCILLATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle is moving in a straight line with uniform velocity. Its acceleration is
ApositiveBnegativeCzeroDnone of these - Question 2 - Select One
A particle is moving in a straight line with uniform velocity. Its acceleration is
ApositiveBnegativeCzeroDnone of these - Question 3 - Select One
A particle is moving on a straight line and its average velocity is found to be zero in an interval of time.
AAverage speed of the particle may also be zero for a given interval of time.BVelocity of the particle can never be zero in given interval of time.CVelocity of the particle must be zero at a particular instant.DAcceleration of particle may be zero.
If the velocity "v" of a particle varies as the square of its displacement "x" then the acceleration varies as
View Solution" If the velocity v of a particle varies as the square of its displacement "x" then the acceleration varies as "
View SolutionA particle starts moving in a straight line with initial velocity v0 Applied forces cases a retardation of av, where v is magnitude of instantaneous velocity and α is a constant.
Total distance covered by the particle isView SolutionA particle is moving on a straight line such that square of its velocity is directly proportional to distance as shown in graph. What is the acceleration of the particle ?
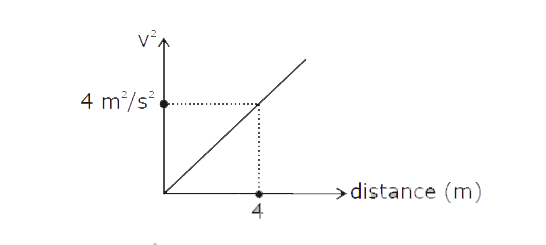 View Solution
View SolutionA particle starts moving in a straight line with initial velocity v0 Applied forces cases a retardation of av, where v is magnitude of instantaneous velocity and α is a constant.
How long the particle will take to come to rest.View Solution

