A particle is moving in a straight line and relationn between time and displacement is t=ax2+βx. If retardation is found to be proportional to the vn, where v is instantaneous velocity, find the value of n.
The correct Answer is:3
t=αx2+βx
⇒dtdx=2αx+β
Hence instantaneous velocity fo the particle can be written as follows :
⇒ v=dxdt=12αx+β ……..(1)
We can differentiate the above relation of velocity to get the acceleration.
⇒ a=dvdt=−1(2αx+β)2×2α×dxdt
In above relation dx//dt is instantaneous velocity v and also we can use equation (1) to rewrite the above relation as follows :
⇒ a=−v2×2α×v
⇒ a=−αv3 .
We can see that n = 3 .
Hence answer is 3.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS )1videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)12videos
OSCILLATIONS
Similar Questions
A particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View Solution
Knowledge Check
- Question 1 - Select One
A particle move in a straight line with retardation proportional to its displacement its loss of kinectic energy for any displacement x is proportional to
AxBe2Cx2Dlogex - Question 2 - Select One
A particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to
Ax2BexCxDlogex - Question 3 - Select One
A particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to
Ax2BexCxDlogex
A particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
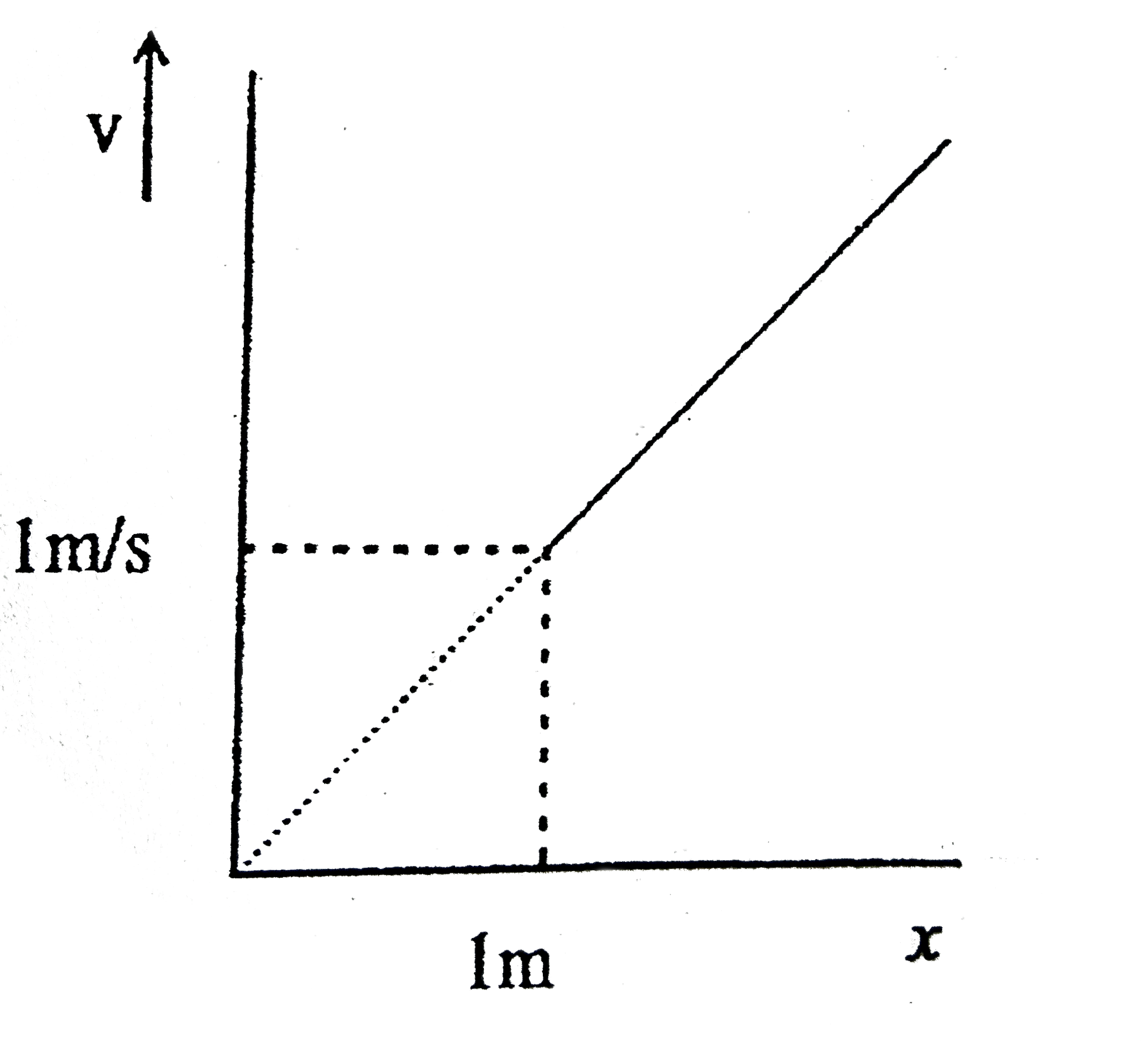 View Solution
View SolutionA body at rest is moved in a stright line by supplying constant power to it . Distance moved by the body in time t is found to be proportional to tn Value of n is .
View SolutionFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
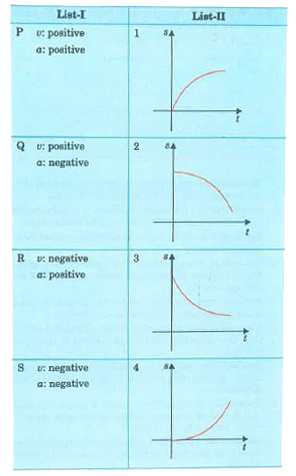 View Solution
View SolutionA particle is moving in a straight line. Its displacement at time t is given by s(Inm)=4t2+2t, then its velocity and acceleration at time t=12 second are
View Solution

