After flying for 18 min in a wind blowing 42 km/h at an angle of south of east, an airplane pilot is over a town that is 55 km due north of the starting point. What is the speed of the airplane relative to the air?
To solve the problem, we need to find the speed of the airplane relative to the air, given the wind speed and direction, as well as the displacement of the airplane.
1. Understanding the Problem:
- The airplane flies for 18 minutes (which we will convert to hours).
- The wind blows at 42 km/h at an angle of 20 degrees south of east.
- The airplane ends up 55 km due north of the starting point.
2. Convert Time to Hours:
- 18 minutes = 18/60 hours = 0.3 hours.
3. Calculate the Wind's Velocity Components:
- The wind's speed is 42 km/h.
- The angle is 20 degrees south of east.
- The components of the wind's velocity can be calculated using trigonometric functions:
- Vwx=42cos(20∘)
- Vwy=−42sin(20∘) (negative because it is south)
- Calculating these:
- Vwx=42×0.9397≈39.46km/h
- Vwy=−42×0.3420≈−14.36km/h
4. Determine the Airplane's Displacement:
- The airplane is 55 km due north of the starting point, which gives us the displacement vector:
- Δx=0km (no east-west displacement)
- Δy=55km
5. Calculate the Airplane's Velocity Relative to the Ground:
- The average velocity of the airplane relative to the ground can be calculated as:
- Vg=ΔyΔt=55km0.3h≈183.33km/h(north)
6. Set Up the Velocity Equation:
- The velocity of the airplane relative to the ground Vg is the vector sum of the airplane's velocity relative to the air Va and the wind's velocity Vw:
- Vg=Va+Vw
- In component form:
- Vgx=Vax+Vwx
- Vgy=Vay+Vwy
7. Substituting Known Values:
- Since the airplane's east-west component is zero (it only moves north):
- Vax+39.46=0 → Vax=−39.46km/h
- For the north component:
- Vay−14.36=183.33 → Vay=183.33+14.36=197.69km/h
8. Calculate the Magnitude of the Airplane's Velocity:
- The speed of the airplane relative to the air can be found using the Pythagorean theorem:
- Va=√V2ax+V2ay
- Va=√(−39.46)2+(197.69)2
- Va=√1557.76+39077.76
- Va=√40635.52≈201.58km/h
Conclusion:
The speed of the airplane relative to the air is approximately 201.58 km/h.
- The airplane flies for 18 minutes (which we will convert to hours).
- The wind blows at 42 km/h at an angle of 20 degrees south of east.
- The airplane ends up 55 km due north of the starting point.
- 18 minutes = 18/60 hours = 0.3 hours.
- The wind's speed is 42 km/h.
- The angle is 20 degrees south of east.
- The components of the wind's velocity can be calculated using trigonometric functions:
- Vwx=42cos(20∘)
- Vwy=−42sin(20∘) (negative because it is south)
- Calculating these:
- Vwx=42×0.9397≈39.46km/h
- Vwy=−42×0.3420≈−14.36km/h
- The airplane is 55 km due north of the starting point, which gives us the displacement vector:
- Δx=0km (no east-west displacement)
- Δy=55km
- The average velocity of the airplane relative to the ground can be calculated as:
- Vg=ΔyΔt=55km0.3h≈183.33km/h(north)
- The velocity of the airplane relative to the ground Vg is the vector sum of the airplane's velocity relative to the air Va and the wind's velocity Vw:
- Vg=Va+Vw
- In component form:
- Vgx=Vax+Vwx
- Vgy=Vay+Vwy
- Since the airplane's east-west component is zero (it only moves north):
- Vax+39.46=0 → Vax=−39.46km/h
- For the north component:
- Vay−14.36=183.33 → Vay=183.33+14.36=197.69km/h
- The speed of the airplane relative to the air can be found using the Pythagorean theorem:
- Va=√V2ax+V2ay
- Va=√(−39.46)2+(197.69)2
- Va=√1557.76+39077.76
- Va=√40635.52≈201.58km/h
The speed of the airplane relative to the air is approximately 201.58 km/h.
Topper's Solved these Questions
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
49 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
3 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT
3 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
Similar Questions
A plane moves in windy weather due east while the pilot the plane somewhat south of east. The wind is blowing at 50 km/h directed 30∘ east of north, while the palne moves at 200 km/h relative to the wind . What is the velocity of the plane relative to the ground and what is the direction in which the pilot points the palne ?
View SolutionAn aeroplane takes off from Mumbai to Delhi with velocity 50 kph at an angle 30∘ north of east. Wind is blowing at 25 kph from north to south. What is the resultant displacement of aeroplane in 2 hrs. (in km)
View Solution
Knowledge Check
A motorboat travels 10 km. upstream in the stream which is following at a speed of 2 km./hr. and returns to starting point in 55 min. What is the speed of motorboat in still water ?
A24 km./hourB22 km./hourC32 km./hourD28 km./hourAn aircraft flies at 400km/h in still air. A wind of 200√2km/h is blowing from the south towards north. The pilot wishes to travel from A to a point B north east of A. Find the time of his journey if AB=1000km.
At=0.83hBt=1.83hCt=2.83hD1A man swims across the river which flows with a velocity of 3 km/h due east. If the velocity of man relative to water is 4 km/h due north, then what is his velocity and its direction relative to the shore of the river?
A4 km/h, 63∘50' west of northB5 km/h, 36∘52' west of northC4 km/h, 63∘50' east of northD5 km/h, 36∘52' east of north
The shock wave off the cockpit of the FA 18 has an angle of about 60∘ . The airplane was traveling at about 1350 km/h when the photograph was taken. Approximately what was the speed of sound at the air plane's altitude?
View SolutionA plane is travelling eastward at a speed of 500kmh−1. But a 90kmh−1 wind is blowing southward. What is the direction and speed of the plane relative to the ground ?
View SolutionA car travles 6km towards north at an angle of 45∘ to the east and then travles distance of 4km towards north at an angle of 135∘ to east (figure). How far is the point from the starting point? What angle does the straight line joining its initial and final position makes with the east?
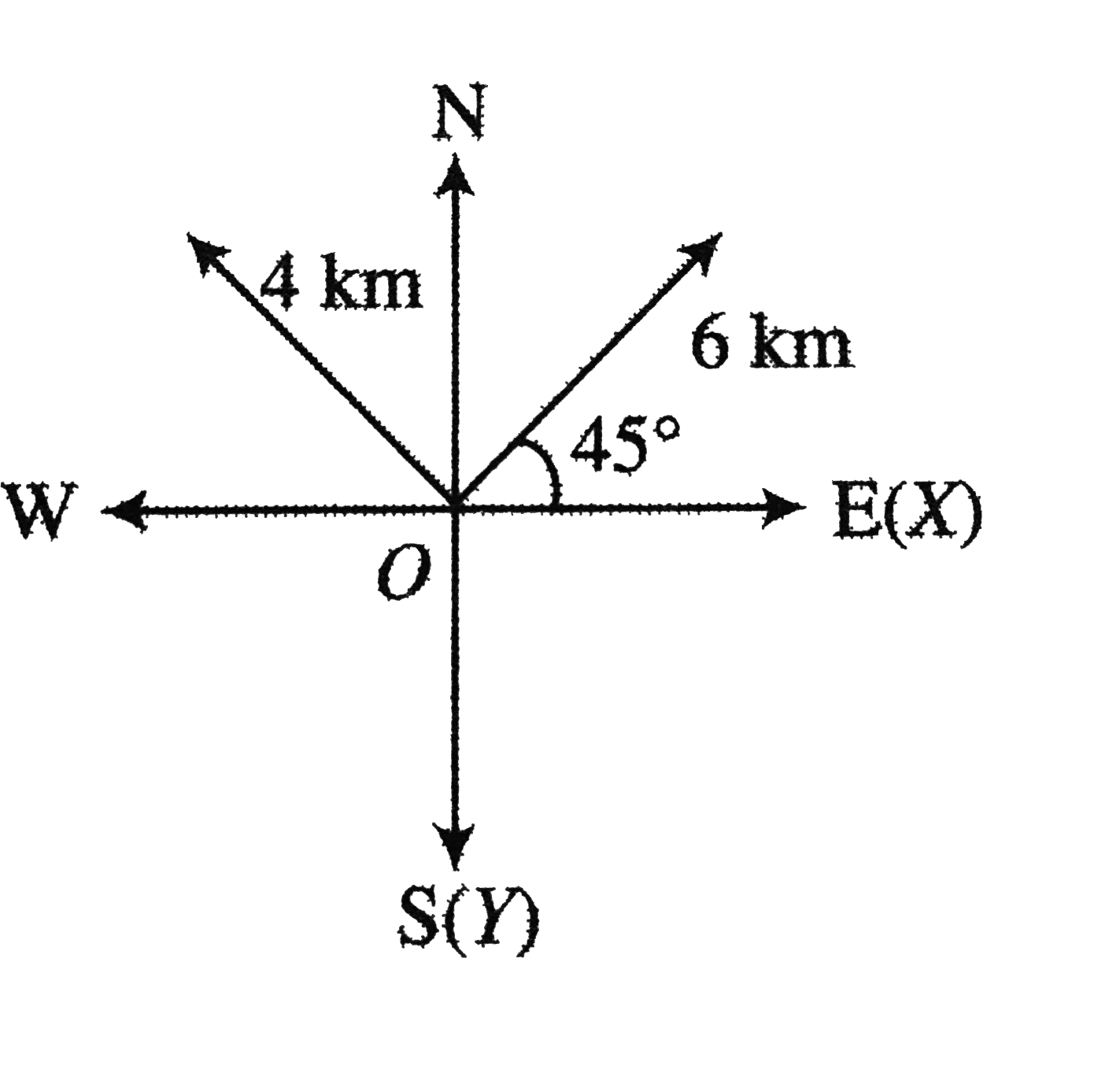
View SolutionAn aeroplane pilot wishes to fly due west A wind of 100kmh−1 is blowing towards south.
(a) If the speed of the plane (its speed in still air) is 300kmh−1 in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.
View SolutionAircraft experience a lift force (due to air) that is perpendicular to the plane of the wings A small airplane is flying at a constant speed of 280 kph At what angle from the horizontal must the wings of the airplane be tilted for the plane to execute a horizontal turn from east to north with a turning radius of 1200 m ?
View Solution
