A ball is to be shot from level ground toward a wall at distance x. Figure 4-36b shows the y component vy of the ball's velocity just as it would reach the wall, as a function of that distance x. The scaling is set by vys=5.0m/sandxs=20m. What is the launch angle?
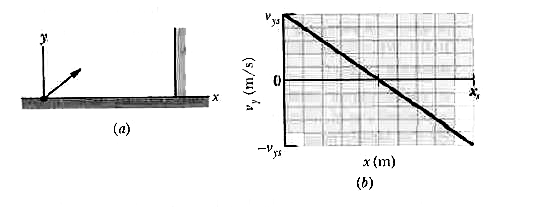
14.3∘≈14∘
Topper's Solved these Questions
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
49 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
3 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT
3 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
Similar Questions
A ball is thrown from ground level so as to just clear a wall 4m high at a distance of 4 m and falls at a distance of 14 m from the wall. Find the magnitude and direction of the initial velocity.
View SolutionA ball is thrown from the ground towards a wall of height h at a distance d1 such that it just clears the wall and falls at a distance d2 on the other side of the wall.If angle of projection is 450 ,find h in terms of d1 and d2.
View Solution
Knowledge Check
A ball is thrown from the ground so as to just clear a wall 10m high at a distance of 20m and falls at a distance of 40m from the wall. The magnitude and direction of the projection velocity is
A10m/s,30∘B25m/s,60∘C25m/s,tan−1(3/4)D10m/s,tan−1(3/4)A ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
ABall will return to ground at t=2v0sinθgBd=e(R−L)(whereRisv0sin2θg)Cmaximum height during motion =v20sin2θ2gDit will return to ground at t<2v0sinθg
A ball is thrown from ground level so as to just clear a wall 4 m high at a distance of 4 m and fall at a distance of 14 m from the wall. Find the magnitude and direction of the velocity of the ball.
View SolutionA ball is thrown from the ground to clear a wall 3m high at a distance of 6m and falls 18m away from the wall, the angle of projection of ball is tan−1(2x). Find value of x.
View SolutionA ball is thrown from the ground level so as to just clear a wall 8 m high at a distance of 4 m and falls at a distance of 14 m from the wall. The magnitude and direction of the velocity of the ball are √(182) m. p.s. and tan−19/7
View SolutionA particle is projected from ground towards a vertical wall 80 m away at an angle of 37∘ with horizontal with initial velocity of 50 m/s. after its collision with wall & then once with rgound find at what distance in meter from wall will it strike the ground. The component of velocity normal to the surface becomes half after collision with cach surface.
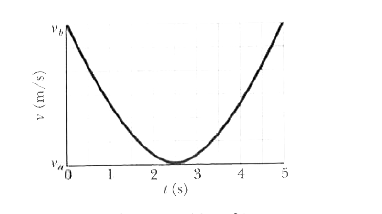
View SolutionA golf ball is struck at ground level. The speed of the golf ball as a function of the time is shown in, where t = 0 at the instant the ball is struck. The scaling on the vertical axis is set by va=19m/sandvb=31m/s. (a) How far does the golf ball travel horizontally before returning to ground level? (b) What is the maximum height above ground level attained by the ball?
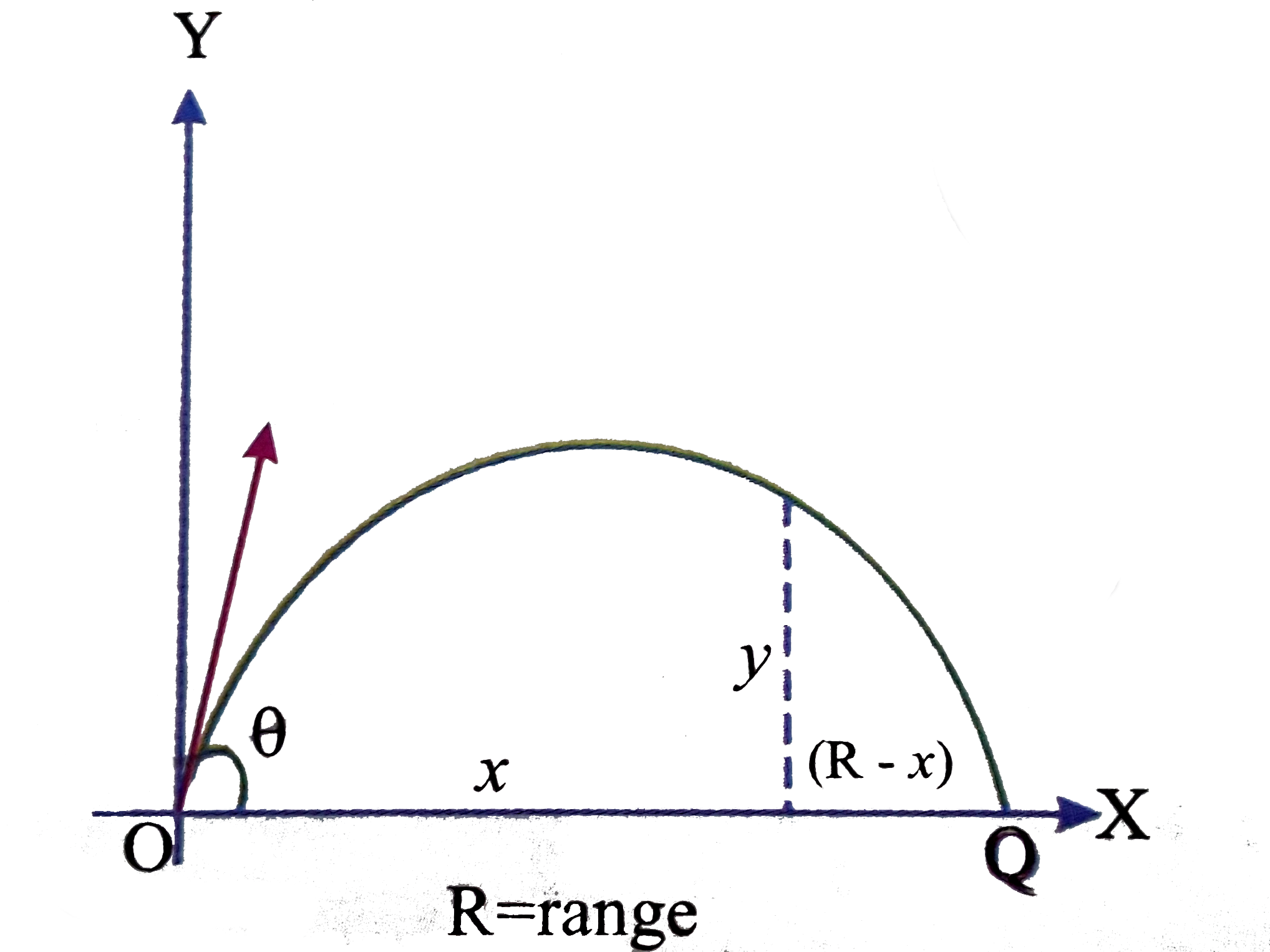
View SolutionA body projected from a point O at an angle θ, just crosses a wall y m high at a distance. x m from the point of projection and strikes the ground at Q beyond the wall as shown, then find height of the wall
View Solution
