In the overhead view of Fig. 4-40, Jeeps P and B race along straight lines, across flat terrain, and past stationary border guard A. Relative to the guard, B travels at a constant speed of 25.0 m/s, at the angle θ2=30.0∘. Relative to the guard, P has accelerated from rest at a constant rate of 0.400m/s2 at the angle θ1=60.0∘. At a certain time during the acceleration, P has a speed of 40.0 m/s. At that time, what are the (a) magnitude and (b) direction of the velocity of P relative to B and the ( c) magnitude and (d) direction of the acceleration of P relative to B?

(a) 22.2 m/s, (b) −85.7∘, which is 85.7 north of west, ( c) 0.400m/s2, (d) 60.0∘ north of due east (or 30.0∘ east of north)
Topper's Solved these Questions
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
49 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
3 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT
3 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
Similar Questions
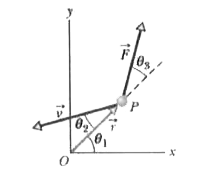
At the instant of Figure, a 2.0 kg particle P has a position vector →r of magnitude 5.0 m and angle θ1=45∘ and a velocity vector →v of magnitude 4.0 m/s and angle θ2=30∘, Force →F, of magnitude 2.0 N and angle θ3=30∘, acts on P. All three vectors lie in the xy plane. About the origin, what are the (a) magnitude and (b) direction of the angular momentum of P and the ( c) magnitude and (d) direction of the torque acting on P?
View SolutionAt one instant a bicyclist is 30.0 m due east of a park's flagpole, going due south with a speed of 10.0 m/s. Then 30.0 s later, the cyclist is 40.0 m due north of the flagpole, going due east with a speed of 10.0 m/s. For the cyclist in this 30.0 s interval, what are the (a) magnitude and (b) direction of the displacement, the ( c) magnitude and (d) direction of the average velocity, and the (e) magnitude and (f) direction of the average acceleration?
View Solution
Knowledge Check
A car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
AIts maximum speed is 8ms−1BIts maximum speed is 6ms−1CIt travelled a total distance of 24mDIt travelled a total distance of 18mTwo boats are heading away from shore. Boat 1 heads due north at a speed of 3.00 m/s relative to the shore. Relative to Boat 1, Boat 2 is moving 30.0∘ north of east at a speed of 1.60 m/s. A passenger on Boat 2 walks due east across the deck at a speed of 1.20 m/s relative to Boat 2. What is the speed of the passenger relative to the shore?
A4.60 m/sB2.71 m/sC2.53 m/sD3.14 m/s
A motorboat starting from rest on a lake acceleration line at a constant rate of 3.0m/s2 for 8.0s. How far does the boat travel during this time ?
View SolutionLift travels in straight line at a constant speed of 3108m/s. What is the acceleration of lift ?
View SolutionAn object having a velocity 4.0 m/s is accelerated at the rate of 1.2ms2 for 5.0s. Find the distance travelled during the period of acceleration.
View SolutionA particle starting from rest has a constant acceleration of 4m/s2 for 4 s. It then retards uniformly for next 8 s and comes to rest. Find during the motion of particle (a) average acceleration (b) average speed and (c) average velocity.
View SolutionA car starts from rest and moves around a circular track of radius 32.0 m. Its speed increases at the constant rate of 0.600m/s2. (a) What is the magnitude of its net linear acceleration 15.0 s later? (b) What angle does this net acceleration vector make with the car's velocity at this time?
View SolutionA particle P is moving along a straight line with a velocity of 3ms−1 and another particle Q has a velocity of 4ms−1 at an angle of 30∘ to the path of P. Find the speed of Q relative to P.
View Solution
