Condition for autocollimation
Find the distance between the convex lens and convex mirror, both of focal length 20cm (Figs. 34-42a and b ), so that for an object kept at 30cm from the lens, the final image is at the object itself. (This is commonly known as condition for autocollimation that we discussed in Section 33.5)
(1) This condition occurs when the object and image coincide. In the case of mirror, this happens when the object for the mirror is at its pole or at the center of curvature (Figs. 34-42a and b). In the second case, the angle of incidence is 0∘ and hence the angle of reflection will also be 0∘.
(2) In the case of single lens, image can never coincide with the object because the rays are refracted into the next medium. But if the lens is kept before the mirror, after refraction from the lens, rays will fall on the mirror. If the image of the lens is at th pole or at the center
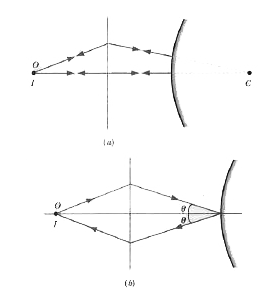
of the curvature of the mirror, the rays will retrace their path and hence by the principle of optical reversibility, we can say that image will again form on the object.
Calculation : For the lens ,
v=ufu+f=20×−30−30+20=60cm
For the mirror, this image should act as an object. The autocollimation will occur if this image is formed at pole. In this situation, the distance between the lens and the pole will be 60cm
Autocollimation will also occur if this image is formed at the center of curvature of the mirror. But the center of curvature is 40cm away from the pole as can be seen in the figure. So, the lens can also be at 60-40=20cm from the mirror.
Learn : In fact, a beam of light can be made to retrace its path by using a transparent sphere silvered at its back. For this the condition of autocollimation requires that the intermediate image which acts as an object for the mirror at the back is at the center of the sphere (Fig. 34-43b) or at its pole (Fig. 34-43a). It is obvious that due to refraction from a sphere, image cannot be formed at its center (angle of refraction will become zero for a finite angle of incidence as can be
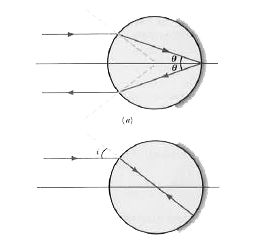
seen in Fig. 35-43b). But the image due to refraction at the curved surface can be definitely formed at the pole of the mirror.
This would happen if the refrective index of the sphere is exactly two times the refractive index of the medium from which the radiation is incident.
Note : This is conventionally known as a cat.s eye retroreflector. The term cat.s eye derives from the resembalance of the cat.s eye retroreflector to the optical system that produces the well-known phenomenon of "glowing eyes " or eye shine in cats and other vertebrates (which are only reflecting light, rather than actually glowing).
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBook:RESNICK AND HALLIDAYChapter:GEOMETRICAL OPTICS : REFRACTIONExercise:Check point
Explore 6 Videos
- GEOMETRICAL OPTICS : REFRACTIONBook:RESNICK AND HALLIDAYChapter:GEOMETRICAL OPTICS : REFRACTIONExercise:Problems
Explore 44 Videos
- GEOMETRICAL OPTICS : REFLECTION Book:RESNICK AND HALLIDAYChapter:GEOMETRICAL OPTICS : REFLECTION Exercise:PRACTICE QUESTIONS (Integer Type)
Explore 3 Videos
- GRAVITATIONBook:RESNICK AND HALLIDAYChapter:GRAVITATIONExercise:PRACTICE QUESTIONS (INTEGER TYPE)
Explore 4 Videos
Similar Questions
An optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
View SolutionFind distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirrorA convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirrorAn object is kept at a distance 20 cm from a convex mirror of focal length 20 cm. The image will form at
AinfinityBfocusCthe position of objectD10 cm behind the mirror
Find distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionA biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
View SolutionAn optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
View SolutionA biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
View Solution
