Find distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.
The correct Answer is:B, C
To solve the problem of finding the distance of the image from a convex lens and the magnification, we can follow these steps:
Step 1: Identify the given values
- Focal length of the lens (F) = +20 cm (positive for convex lens)
- Object distance (u) = -30 cm (negative as per sign convention)
Step 2: Use the lens formula
The lens formula is given by:
1F=1V−1U
We need to find the image distance (V).
Step 3: Substitute the values into the lens formula
Substituting the known values into the formula:
120=1V−1−30
This simplifies to:
120=1V+130
Step 4: Rearrange the equation to find V
Rearranging gives:
1V=120−130
Step 5: Find a common denominator and simplify
The least common multiple (LCM) of 20 and 30 is 60. Therefore, we can rewrite the fractions:
120=360,130=260
Substituting these values back:
1V=360−260=160
Step 6: Solve for V
Taking the reciprocal gives:
V=60 cm
Step 7: Determine the nature of the image
Since V is positive, the image is formed on the opposite side of the lens from the object, indicating that it is a real image.
Step 8: Calculate the magnification (M)
The magnification is given by the formula:
M=VU
Substituting the values:
M=60−30=−2
Step 9: Interpret the magnification
The negative sign indicates that the image is inverted, and the magnitude of 2 indicates that the image is twice the size of the object.
Final Results
- Distance of the image from the lens (V) = 60 cm
- Magnification (M) = -2 (indicating a real, inverted image that is 2 times larger than the object)
---
- Focal length of the lens (F) = +20 cm (positive for convex lens)
- Object distance (u) = -30 cm (negative as per sign convention)
The lens formula is given by:
1F=1V−1U
We need to find the image distance (V).
Substituting the known values into the formula:
120=1V−1−30
This simplifies to:
120=1V+130
Rearranging gives:
1V=120−130
The least common multiple (LCM) of 20 and 30 is 60. Therefore, we can rewrite the fractions:
120=360,130=260
Substituting these values back:
1V=360−260=160
Taking the reciprocal gives:
V=60 cm
Since V is positive, the image is formed on the opposite side of the lens from the object, indicating that it is a real image.
The magnification is given by the formula:
M=VU
Substituting the values:
M=60−30=−2
The negative sign indicates that the image is inverted, and the magnitude of 2 indicates that the image is twice the size of the object.
- Distance of the image from the lens (V) = 60 cm
- Magnification (M) = -2 (indicating a real, inverted image that is 2 times larger than the object)
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 10
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 11
3 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Draw a labelled ray diagram for the formation of image by a convex lens of focal length 15 cm when the object is placed at a distance of 25 cm from the lens. Determine the size of the image formed, if size of the object is 4 cm.
View SolutionThe plane surface of a plano-convex lens of focal length 60 cm is silvered. A point object is placed at a distance 20 cm from the lens. Find the position and nature of the final image formed.
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
An object of height 2 cm is placed in front of a convex lens of focal length 20 cm at a distance of 15 cm from it. Find the position and magnification of the image.
View SolutionIn an experiment for the determination of focal length of the convex mirror a convex lens of focal length 20cm is placed on the optical bench and an object pin is placed at a distance 30cm from the lens. When a convex mirror is introduced in between the lens and the real and inverted image of the object, the final image of object O is formed at O itself. If the distance between the lens and the mirror is 10cm, then the focal length of the mirror is
View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionA point object O is placed at a distance of 20cm from a convex lens of focal length 10cm as shown in the figure. At what distance x from the lens should a convex mirror of focal length 60cm, be placed so that final image coincide with the object?

View SolutionA point object O is placed at a distance of 20 cm from a convex lens of focal length 10 cm as shown in figure. At what distance x from the lens should a concave mirror of focal length 60 cm, placed so that final image coincides with the object ?

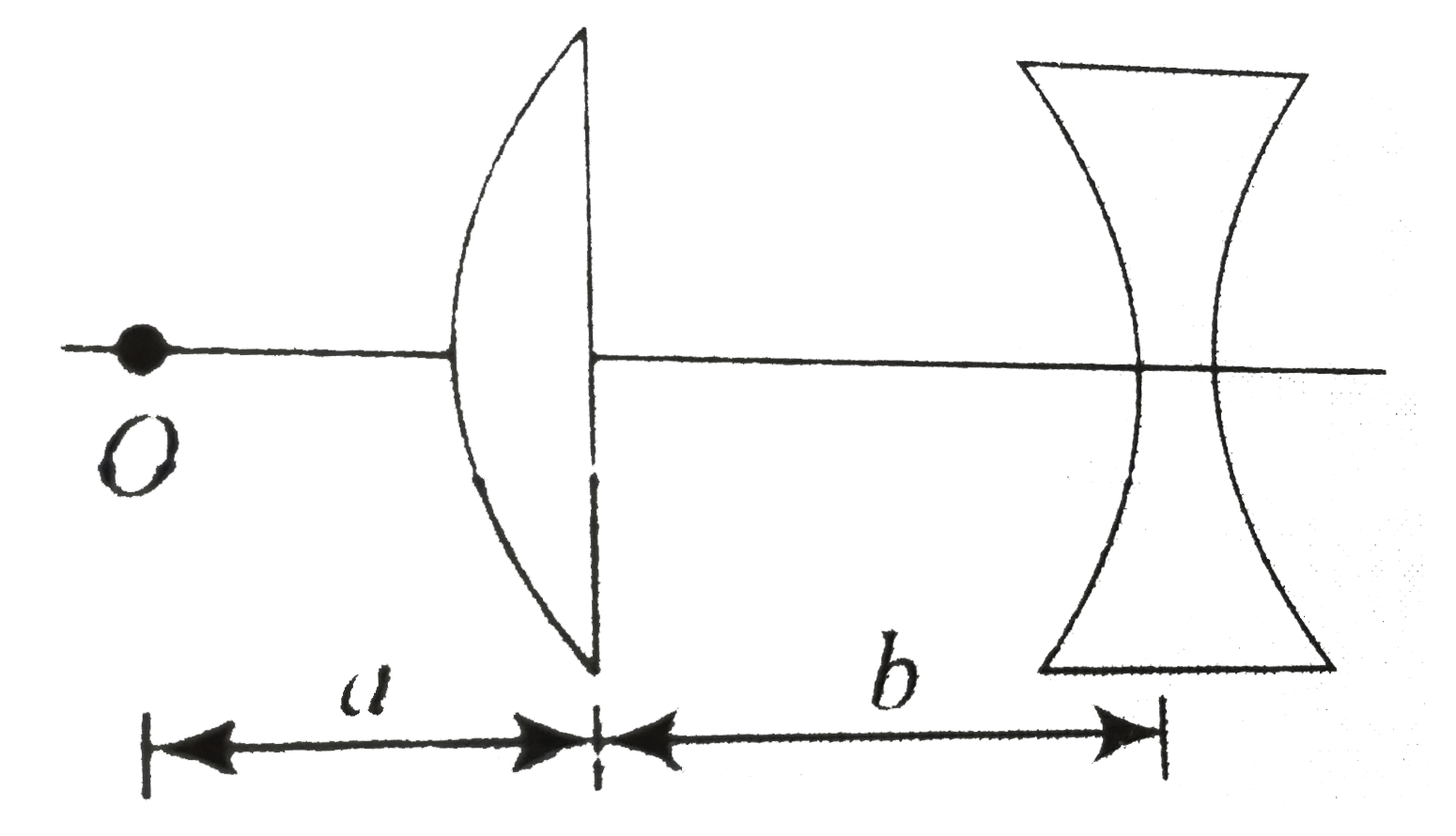
View SolutionA plano-convex glass lens (μg=3/2) of radius of curvatureR=10cm is placed at a distance of b from a concave lens of focal length 20cm. What should be the distance a of point object O from the plano-convex lens so that position of final image is independent of b?
View SolutionDistance of an object from a concave lens of focal length 20 cm is 40 cm. Then linear magnification of the image
View Solution
