An optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
60cm
30cm
75cm
45cm
The correct Answer is:B
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the given data
- Focal length of the convex lens (F) = +30 cm (positive for convex lens)
- Distance of the plane mirror from the lens = 15 cm
- Object distance from the lens (U) = -15 cm (negative as per sign convention)
Step 2: Use the lens formula to find the position of the first image
The lens formula is given by:
1F=1V−1U
Substituting the known values:
130=1V1−1−15
This simplifies to:
130=1V1+115
To solve for V1, we first find a common denominator:
130=1V1+230
Rearranging gives:
1V1=130−230=−130
Thus, we find:
V1=−30 cm
This means the first image is formed 30 cm to the left of the lens.
Step 3: Determine the object distance for the mirror
The distance from the lens to the mirror is 15 cm. Since the first image is 30 cm to the left of the lens, the distance from the image to the mirror (acting as a new object for the mirror) is:
Distance from image to mirror=30 cm+15 cm=45 cm
Thus, the object distance for the mirror (U2) is:
U2=−45 cm
Step 4: Use the mirror formula to find the position of the second image
The mirror formula is similar to the lens formula:
1F=1V−1U
For a plane mirror, the focal length (F) is considered infinite, thus:
0=1V2−1−45
This simplifies to:
1V2=145
Thus, we find:
V2=+45 cm
This means the second image is formed 45 cm behind the mirror.
Step 5: Determine the object distance for the lens again
The second image (acting as an object for the lens) is now 45 cm behind the mirror. Since the mirror is 15 cm behind the lens, the total distance from the lens to the new object is:
Distance from lens to new object=15 cm+45 cm=60 cm
Thus, the object distance for the lens (U3) is:
U3=−60 cm
Step 6: Use the lens formula again to find the final image position
Using the lens formula again:
130=1V3−1−60
This simplifies to:
130=1V3+160
Finding a common denominator gives:
130=260+1V3
Rearranging gives:
1V3=130−260=130−130=0
Thus, we find:
V3=+60 cm
This means the final image is formed 60 cm to the right of the lens.
Step 7: Calculate the distance between the object and the final image
The object is located 15 cm in front of the lens, and the final image is located 60 cm behind the lens. Therefore, the distance between the object and the final image is:
Distance=60 cm−(−15 cm)=60+15=75 cm
Final Answer
The distance of the final image from the object is 75 cm.
- Focal length of the convex lens (F) = +30 cm (positive for convex lens)
- Distance of the plane mirror from the lens = 15 cm
- Object distance from the lens (U) = -15 cm (negative as per sign convention)
The lens formula is given by:
1F=1V−1U
Substituting the known values:
130=1V1−1−15
This simplifies to:
130=1V1+115
To solve for V1, we first find a common denominator:
130=1V1+230
Rearranging gives:
1V1=130−230=−130
Thus, we find:
V1=−30 cm
This means the first image is formed 30 cm to the left of the lens.
The distance from the lens to the mirror is 15 cm. Since the first image is 30 cm to the left of the lens, the distance from the image to the mirror (acting as a new object for the mirror) is:
Distance from image to mirror=30 cm+15 cm=45 cm
Thus, the object distance for the mirror (U2) is:
U2=−45 cm
The mirror formula is similar to the lens formula:
1F=1V−1U
For a plane mirror, the focal length (F) is considered infinite, thus:
0=1V2−1−45
This simplifies to:
1V2=145
Thus, we find:
V2=+45 cm
This means the second image is formed 45 cm behind the mirror.
The second image (acting as an object for the lens) is now 45 cm behind the mirror. Since the mirror is 15 cm behind the lens, the total distance from the lens to the new object is:
Distance from lens to new object=15 cm+45 cm=60 cm
Thus, the object distance for the lens (U3) is:
U3=−60 cm
Using the lens formula again:
130=1V3−1−60
This simplifies to:
130=1V3+160
Finding a common denominator gives:
130=260+1V3
Rearranging gives:
1V3=130−260=130−130=0
Thus, we find:
V3=+60 cm
This means the final image is formed 60 cm to the right of the lens.
The object is located 15 cm in front of the lens, and the final image is located 60 cm behind the lens. Therefore, the distance between the object and the final image is:
Distance=60 cm−(−15 cm)=60+15=75 cm
The distance of the final image from the object is 75 cm.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions1videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective29videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason13videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
An object O is kept infront of a converging lens of focal length 30 cm behind which there is a plane mirror at 15 cm from the lens.
_E01_080_Q01.png) View Solution
View SolutionTwo thin lenses, both of 10 cm focal length- one convex and other concave, are placed 5 cm apart. An object is placed 20 cm in front of the convex lens. Find the nature and position of the final image.
View Solution
Knowledge Check
- Question 1 - Select One
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
An optical system consists of two convergent lenses with focal length f1=20cmandf2=10cm. The distance between the lenses is d=30cm. An object is placed at a distance of 30cm from the first lens. At what distance from the second lens will the images be obtained ?
View SolutionThe plane surface of a plano-convex lens of focal length 60 cm is silvered. A point object is placed at a distance 20 cm from the lens. Find the position and nature of the final image formed.
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
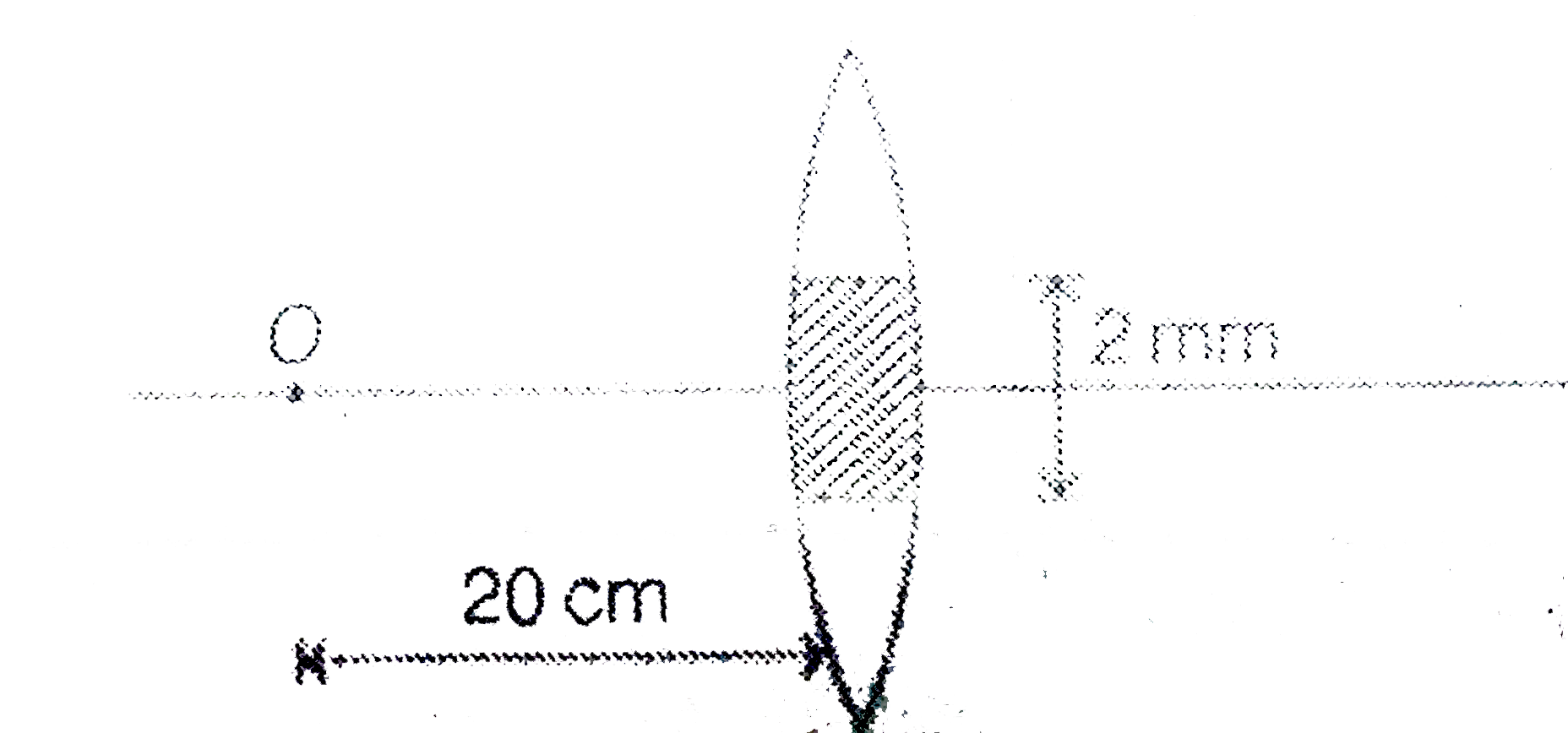 View Solution
View SolutionA biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
View SolutionA convex lens of focal length 10cm is placed 30 cm in front of a second convex lens also of th esame focal length. A plane mirror is placed after the two lenses. Where should a point object be placed in front of the first lens so that it imagees on to itself?
View SolutionIn Figure ., L is a converging lens of focal length 10cm and M Iis a concave mirror of radius of curvature 20cm. A point object O is placed in front of the lens at a distance of 15cm. Ab and CD are optical axes of the lens and mirror, respectively. Find the distance of the final image formed by this system from the optical center of the lens. The distance between CD and AB is 1cm.
 View Solution
View SolutionAn object, a convex lens of focal length 20cm and a plane mirror are arranged as shown in the figure. How far behind the mirror is the second image formed?
 View Solution
View Solution

