AB is a diameter of the circumcircle of ΔAPB, N is the foot of the perpendicular drawn from the point P on AB. If AP=8 cm and BP = 6cm , then the length of BN is
3.6 cm
3 cm
3.4 cm
3.5 cm
The correct Answer is:A
To solve the problem step by step, we will use the properties of triangles and the Pythagorean theorem.
Given:
- AP=8 cm
- BP=6 cm
- AB is the diameter of the circumcircle of triangle ΔAPB
- N is the foot of the perpendicular from point P to line AB
To Find:
- Length of BN
Step 1: Find the length of AB
Since A and B are endpoints of the diameter and P lies on the circle, we can use the Pythagorean theorem in triangle APB.
Using the Pythagorean theorem:
AB2=AP2+BP2
Substituting the given values:
AB2=82+62=64+36=100
Thus,
AB=√100=10 cm
Step 2: Set up the relationship between segments
Let BN=x. Then, since AB=10 cm,
AN=AB−BN=10−x
Step 3: Use the Pythagorean theorem in triangles APN and PBN
In triangle APN:
AP2=AN2+PN2
Substituting the known values:
82=(10−x)2+PN2
This simplifies to:
64=(10−x)2+PN2(1)
In triangle PBN:
PB2=BN2+PN2
Substituting the known values:
62=x2+PN2
This simplifies to:
36=x2+PN2(2)
Step 4: Solve the equations
From equation (2), we can express PN2:
PN2=36−x2(3)
Substituting equation (3) into equation (1):
64=(10−x)2+(36−x2)
Expanding (10−x)2:
64=100−20x+x2+36−x2
This simplifies to:
64=136−20x
Rearranging gives:
20x=136−64
20x=72
x=7220=3.6 cm
Conclusion
The length of BN is 3.6 cm.
- AP=8 cm
- BP=6 cm
- AB is the diameter of the circumcircle of triangle ΔAPB
- N is the foot of the perpendicular from point P to line AB
- Length of BN
Since A and B are endpoints of the diameter and P lies on the circle, we can use the Pythagorean theorem in triangle APB.
AB2=AP2+BP2
Substituting the given values:
AB2=82+62=64+36=100
Thus,
AB=√100=10 cm
Let BN=x. Then, since AB=10 cm,
AN=AB−BN=10−x
In triangle APN:
AP2=AN2+PN2
Substituting the known values:
82=(10−x)2+PN2
This simplifies to:
64=(10−x)2+PN2(1)
PB2=BN2+PN2
Substituting the known values:
62=x2+PN2
This simplifies to:
36=x2+PN2(2)
From equation (2), we can express PN2:
PN2=36−x2(3)
64=(10−x)2+(36−x2)
Expanding (10−x)2:
64=100−20x+x2+36−x2
This simplifies to:
64=136−20x
Rearranging gives:
20x=136−64
20x=72
x=7220=3.6 cm
The length of BN is 3.6 cm.
Similar Questions
AB is the diameter of circumscribe ΔAPB. From the point P there is point N which is the perpendicular on the base AB is. If AP = 8 cm. and BP = 6 cm., then the long of BN = ?
View SolutionABC is a triangle right angled at C. Let p be the length of the perpendicular drawn from C on AB. If BC = 6 cm and CA = 8 cm, then what is the value of p ?
View Solution
Knowledge Check
- Question 1 - Select One
The length of the foot of perpendicular drawn from
the point P(3, 6, 7) on y-axis isA√48B√45C3D√58 - Question 2 - Select One
In the given figure, AP bisects ∠BAC. If AB=4cm, AC=6cm and BP=3cm, then the length of CP is:
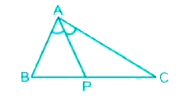 A4.5cmB3cmC5cmD7cm
A4.5cmB3cmC5cmD7cm - Question 3 - Select One
O is the centre of a circle. AB is a chord of the circle but not its diameter. OC is perpendicular to AB. If OC = CB and radius of the circle be 7 cm, then the length of AB is
A7√2cmB14cmC7 cmD7√2 cm
.In given figure OC is perpendicular segment drawn from centre O to chord AB. If OB=5 cm and OC= 3cm then find the length of AB
View SolutionAB is a diameter of circle. P is point on circle and a perpendicular line is drawn on AB at N from it. If radius is 7 cm. and PB = 12 cm. then BN is (in cm)-
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View SolutionIn the given figure, AB is a diameter of a circle and CD is perpendicular to AB, if AB = 10 cm and AE = 2 cm, then what is the length of ED ?
 View Solution
View SolutionABC is an isosceles triangle such that AB=BC=8cm and ∠ABC=90∘ What is the length of the perpendicular drawn from B to AC?
View Solution

