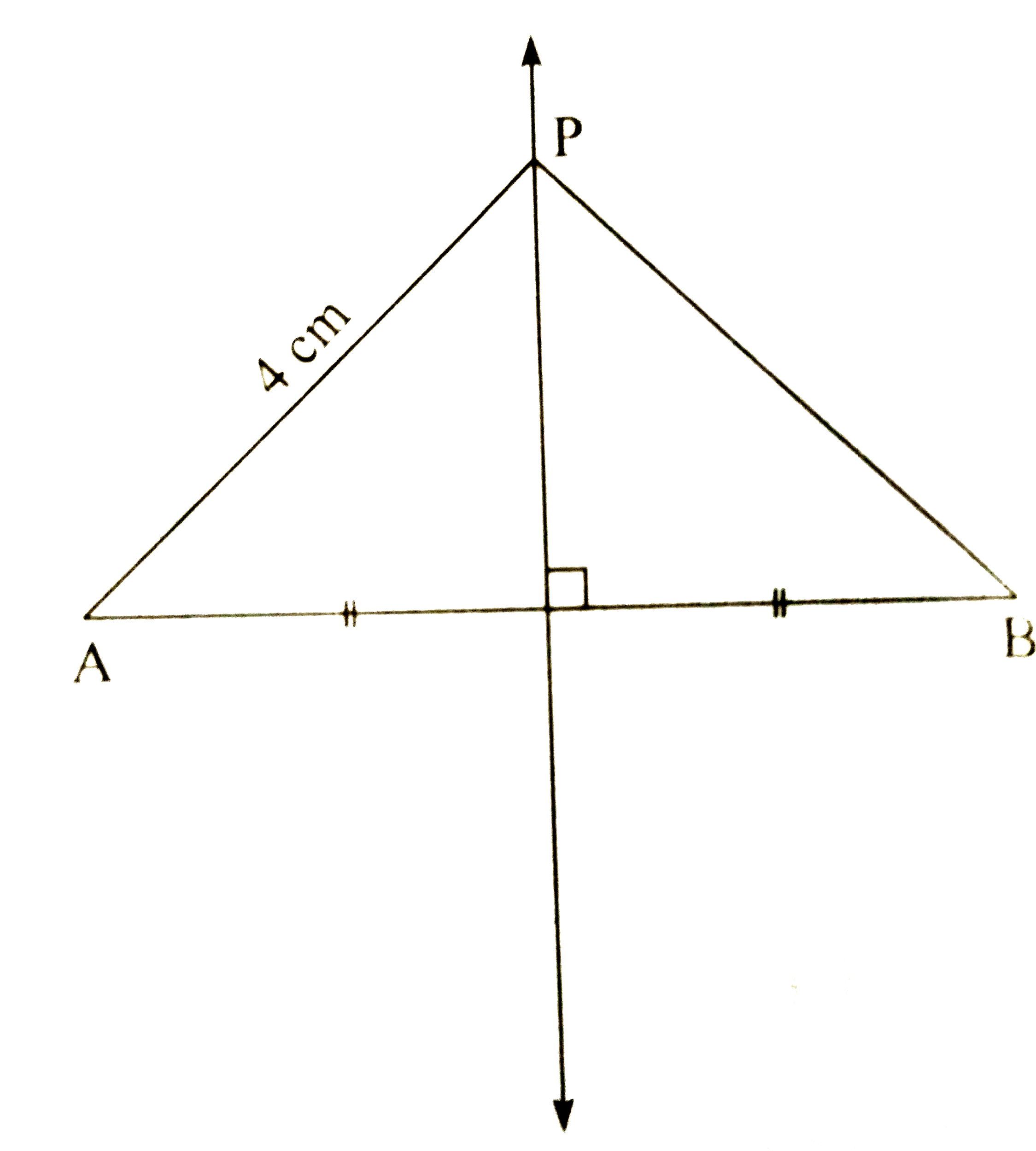
AB is the diameter of circumscribe ΔAPB. From the point P there is point N which is the perpendicular on the base AB is. If AP = 8 cm. and BP = 6 cm., then the long of BN = ?
a)3.6 cm
b)3 cm
c)3.5 cm
d)3.5 cm
To solve the problem, we need to find the length of BN given that AP=8cm and BP=6cm.
1. Identify the Triangle and its Properties:
- We have triangle APB where AB is the diameter of the circumscribed circle. According to the properties of a triangle inscribed in a semicircle, angle APB is a right angle (90 degrees).
Hint: Remember that any triangle inscribed in a semicircle has a right angle opposite the diameter.
2. Apply the Pythagorean Theorem:
- Since APB is a right triangle, we can apply the Pythagorean theorem to find the length of AB:
AB2=AP2+BP2
Substituting the values:
AB2=82+62=64+36=100
Thus,
AB=√100=10cm
Hint: The Pythagorean theorem relates the lengths of the sides of a right triangle. Make sure to square the lengths correctly.
3. Establish Similar Triangles:
- Triangle APB is similar to triangle PNB because they share angle B and both have a right angle at P. Therefore, we can set up a proportion based on their corresponding sides.
Hint: When two triangles are similar, the ratios of their corresponding sides are equal.
4. Set Up the Proportion:
- The sides of the triangles give us the following proportion:
BNPB=PNAP
- We know PB=6cm and AP=8cm. Let BN=x:
x6=PN8
Hint: Label the unknowns clearly to avoid confusion when setting up equations.
5. Express PN in terms of BN:
- From the right triangle PNB, we can express PN using the Pythagorean theorem:
PN2+BN2=PB2
- Since PB=6cm, we can write:
PN2+x2=62⇒PN2+x2=36
Hint: Always remember to apply the Pythagorean theorem correctly to find the height or other sides.
6. Substitute and Solve:
- Now, we can substitute PN from the proportion into the equation:
PN=8x6=4x3
- Substitute this into the equation:
(4x3)2+x2=36
16x29+x2=36
16x2+9x29=36⇒25x29=36
25x2=324⇒x2=32425⇒x=185=3.6cm
Hint: When solving for x, ensure you simplify fractions and square roots properly.
Final Answer:
Thus, the length of BN is 3.6cm.
- We have triangle APB where AB is the diameter of the circumscribed circle. According to the properties of a triangle inscribed in a semicircle, angle APB is a right angle (90 degrees).
- Since APB is a right triangle, we can apply the Pythagorean theorem to find the length of AB:
AB2=AP2+BP2
Substituting the values:
AB2=82+62=64+36=100
Thus,
AB=√100=10cm
- Triangle APB is similar to triangle PNB because they share angle B and both have a right angle at P. Therefore, we can set up a proportion based on their corresponding sides.
- The sides of the triangles give us the following proportion:
BNPB=PNAP
- We know PB=6cm and AP=8cm. Let BN=x:
x6=PN8
- From the right triangle PNB, we can express PN using the Pythagorean theorem:
PN2+BN2=PB2
- Since PB=6cm, we can write:
PN2+x2=62⇒PN2+x2=36
- Now, we can substitute PN from the proportion into the equation:
PN=8x6=4x3
- Substitute this into the equation:
(4x3)2+x2=36
16x29+x2=36
16x2+9x29=36⇒25x29=36
25x2=324⇒x2=32425⇒x=185=3.6cm
Thus, the length of BN is 3.6cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
AB is a diameter of the circumcircle of ΔAPB, N is the foot of the perpendicular drawn from the point P on AB. If AP=8 cm and BP = 6cm , then the length of BN is
A3.6 cmB3 cmC3.4 cmD3.5 cmIn the given figure, AP bisects ∠BAC. If AB=4cm, AC=6cm and BP=3cm, then the length of CP is:
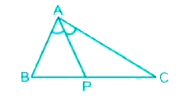 A4.5cmB3cmC5cmD7cm
A4.5cmB3cmC5cmD7cmSuppose AB is a diameter of a circle, whose centre is at O and C be any point on the circle. If CD is perpendicular to AB and CD = 12 cm, AD = 16 cm, then BD is equal to
A10 cmB12 cmC8 cmD9 cm
AB is a diameter of circle. P is point on circle and a perpendicular line is drawn on AB at N from it. If radius is 7 cm. and PB = 12 cm. then BN is (in cm)-
View SolutionChord AB of a circle is produced to a point P, and C is a point on the circle such that PC is a tangent to the circle. If PC = 18 cm, and BP = 15 cm, then AB is equal to:
View SolutionIn ΔABC, the height CD intersects AB at D. The mid-points of AB and BC are P and Q respectively. If AD = 8 cm and CD = 6 cm, then the length of PQ is
View SolutionIn a class of 39 students the ratio of boys and girls is 2 : 1. Radhika ranks 15th among all the students from top and 8th among girls from bottom. How many boys are there below Radhika ?
View SolutionChord AB of a circle is product to a point P and C is a poimt on the circle such that PC is a tangent to the circle. If PC = 18 cm, and BP = 15 cm, then AB is equal to:
View Solution