ABC is a triangle right angled at C. Let p be the length of the perpendicular drawn from C on AB. If BC = 6 cm and CA = 8 cm, then what is the value of p ?
5.4 cm
5 cm
4.8 cm
4.2 cm
To solve the problem, we need to find the length of the perpendicular p drawn from point C to line AB in triangle ABC, which is right-angled at C. We know the lengths of the sides BC=6cm and CA=8cm.
1. Identify the sides of the triangle:
- Given BC=6cm (one leg) and CA=8cm (the other leg).
2. Calculate the length of the hypotenuse AB:
- Using the Pythagorean theorem:
AB2=BC2+CA2
AB2=62+82=36+64=100
AB=√100=10cm
3. Calculate the area of triangle ABC:
- The area A of a right triangle can be calculated using the formula:
A=12×base×height
- Here, we can take BC as the base and CA as the height:
A=12×6×8=482=24cm2
4. Relate the area to the perpendicular p:
- The area can also be expressed in terms of the hypotenuse AB and the perpendicular p:
A=12×AB×p
- Substituting the known values:
24=12×10×p
- Simplifying:
24=5p
p=245=4.8cm
Final Answer:
The value of p is 4.8cm.
---
- Given BC=6cm (one leg) and CA=8cm (the other leg).
- Using the Pythagorean theorem:
AB2=BC2+CA2
AB2=62+82=36+64=100
AB=√100=10cm
- The area A of a right triangle can be calculated using the formula:
A=12×base×height
- Here, we can take BC as the base and CA as the height:
A=12×6×8=482=24cm2
- The area can also be expressed in terms of the hypotenuse AB and the perpendicular p:
A=12×AB×p
- Substituting the known values:
24=12×10×p
- Simplifying:
24=5p
p=245=4.8cm
The value of p is 4.8cm.
Similar Questions
ABC is a triangle right-angled at C. If p is the length of the perpendicular from C to AB and a, b, c are the sides, then which one of the following is correct ?
View SolutionABC is a right traingle, right angled at C. if P is the length of perpendicular from C to AB and AB=c, BC=a and CA=b, then prove that (i) pc=ab (ii) 1p2=1a2+1b2
View Solution
Knowledge Check
ABC is a triangle which is right angled at A and a perpendicular AD is drawn on the hypotenuse BC. If BC = 8 and AD = 3, then what is the value of AB×AC?
A12B24C32D36In a ΔABC right angle at C .P is the length of ⊥ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
A1p2=1b2−1a2B1p2=1a2+1b2C1p2+1a2=−1b2D1p2=1a2−1b2
ABC is a right triangles right angled at C . Let BC =a ,CA=b, AB = c, and p be the length of perpendicular from C to AB . Prove that cp = ab .
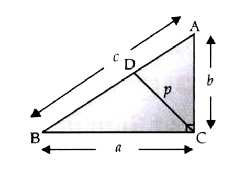
View SolutionABC is a triangle right angled at C with BC = a and AC = b. If p is the length of the perpendicular from C on AB, then which one of the following is correct ?
View SolutionIn a right angled triangle ABC,D is the foot of the perpendicular from B on the hypotenuse AC. If AB=3cm and BC=4cm, what is the area of △ABD
View SolutionIn a right-angled triangle ABC ,D is the foot of the perpendicular from B on the hypotenuse AC . If AB=3cm and BC=4cm, what is the area of △ABD?
View SolutionABC is a triangle right angled at B. If AB=5 cm and BC= 10 cm, then what is the length of the perpendicular drawn from the vertex B to the hypotenuse ?
View SolutionABC is a right triangle right-angled at C . Let BC=a, CA=b, AB=c and let p be the length of perpendicular from C on AB , prove that (i) cp=ab (ii) 1p2=1a2+1b2
View Solution
