Draw a graph of the function $y = [x] + | 1 - x |, - 1 \leq x \leq 3$ . Determine the points if any, where this function is not differentiable.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: ${0, 1, 2)$

$y = [x] + | 1 - x |, - 1 \leq x \leq 3$
$\Rightarrow y = ⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} - 1 + 1 - x, - 1 \leq x < 0 0 + 1 - x, 0 \leq x < 1 1 + x - 1, 1 \leq x < 2 2 + x - 1, 2 \leq x \leq 3 \end{matrix}$
$\Rightarrow y = ⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} - x, - 1 \leq x < 0 1 - x, 0 \leq x < 1 + x, 1 \leq x < 2 x + 1, 2 \leq x < 3 \end{matrix}$
which could be shown as,

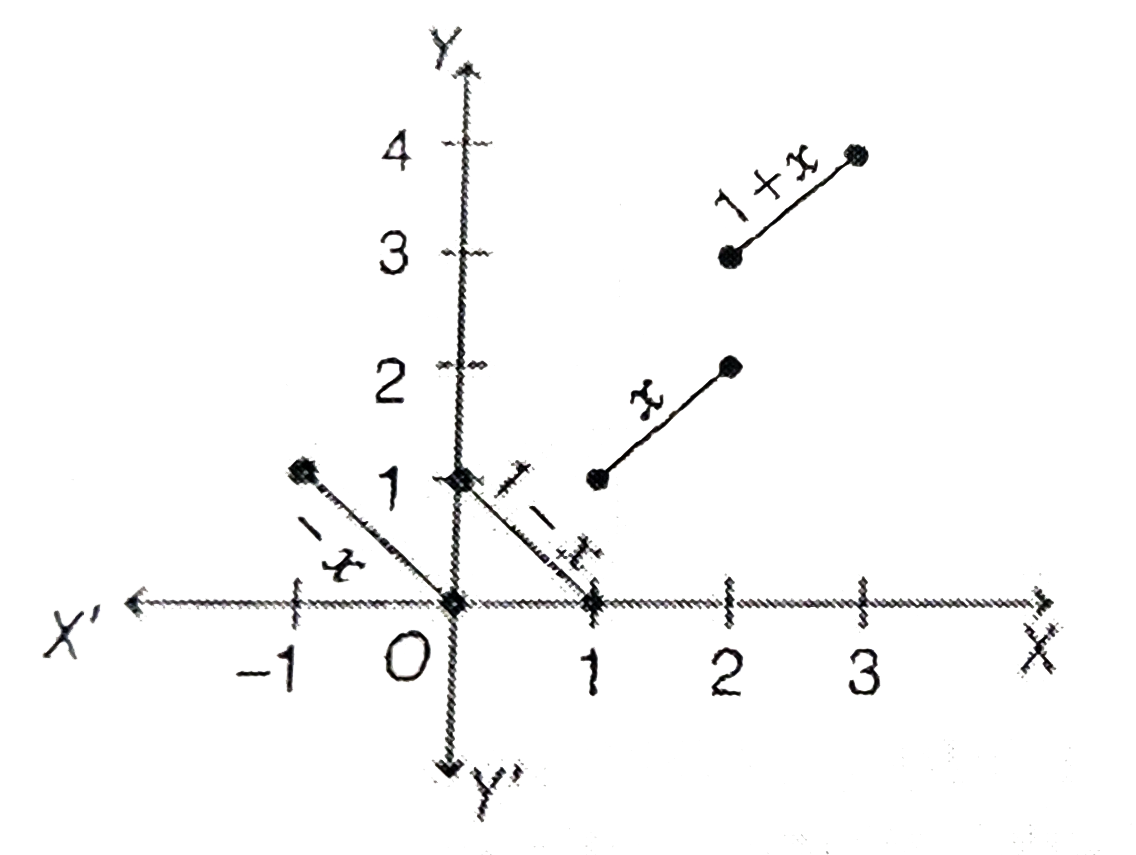
Clearly, from above figure, y is not continuous and not differentiable at $x = {0, 1, 2}$ .

|

Updated on:21/07/2023

Class 12 MATHS LIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The set of points where the function $f (x) = | x - 2 | cos x$ is differentiable is
A $(- \infty, \infty)$
B $(- \infty, 0) \cup (0, \infty)$
C $(0, \infty)$
D $[0, \infty]$
Question 2 - Select One
The set of points where the function $f (x) = x | x |$ is differentiable is
A $(- \infty, \infty)$
B $(- \infty, 0) \cup [0, \infty)$
C $(0, \infty)$
D $[0, \infty)$
Question 3 - Select One
The set of points where the function $f (x) = x | x |$ is differentiable is
A $(- \infty, \infty)$
B $(- \infty, 0) \cup (0, \infty)$
C $(o, \infty)$
D $[0, \infty)$

IIT JEE PREVIOUS YEAR-LIMIT,CONTINUITY AND DIFFERENTIABILITY -Differentiability at a point (Analytical & Descriptive Questions)

Home
Ask Doubt
Profile