A 50 kg ice skater, initially at rest, throws a 0.15 kg snowball with a speed of 35 m/s. What is the approximate recoil speed of the skater?
0.10 m/s
0.20 m/s
0.70 m/s
1.4 m/s
The correct Answer is:A
To solve the problem of the ice skater throwing a snowball and determining the recoil speed of the skater, we can apply the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Identify the masses and initial conditions
- Mass of the ice skater, M=50kg
- Mass of the snowball, m=0.15kg
- Initial speed of both the skater and the snowball, u=0m/s (since both are at rest)
Step 2: Determine the final speed of the snowball
- Speed of the snowball after being thrown, vs=35m/s
Step 3: Apply the conservation of momentum
According to the law of conservation of momentum:
Initial momentum=Final momentum
Since both the skater and the snowball are initially at rest, the initial momentum is:
Initial momentum=0
The final momentum can be expressed as:
Final momentum=mvs+Mvk
where vk is the recoil speed of the skater.
Step 4: Set up the equation
Setting the initial momentum equal to the final momentum:
0=mvs+Mvk
Rearranging gives:
Mvk=−mvs
Step 5: Solve for the recoil speed vk
Substituting the known values:
vk=−mvsM
vk=−0.15kg×35m/s50kg
Step 6: Calculate the value
Calculating the numerator:
0.15×35=5.25kg m/s
Now substituting into the equation:
vk=−5.2550=−0.105m/s
Step 7: Interpret the result
The negative sign indicates that the direction of the skater's recoil speed is opposite to the direction of the snowball's speed. Therefore, the approximate recoil speed of the skater is:
vk≈0.105m/s
Final Answer
The approximate recoil speed of the skater is 0.10m/s (in the opposite direction to the snowball).
---
- Mass of the ice skater, M=50kg
- Mass of the snowball, m=0.15kg
- Initial speed of both the skater and the snowball, u=0m/s (since both are at rest)
- Speed of the snowball after being thrown, vs=35m/s
According to the law of conservation of momentum:
Initial momentum=Final momentum
Since both the skater and the snowball are initially at rest, the initial momentum is:
Initial momentum=0
Final momentum=mvs+Mvk
where vk is the recoil speed of the skater.
Setting the initial momentum equal to the final momentum:
0=mvs+Mvk
Rearranging gives:
Mvk=−mvs
Substituting the known values:
vk=−mvsM
vk=−0.15kg×35m/s50kg
Calculating the numerator:
0.15×35=5.25kg m/s
Now substituting into the equation:
vk=−5.2550=−0.105m/s
The negative sign indicates that the direction of the skater's recoil speed is opposite to the direction of the snowball's speed. Therefore, the approximate recoil speed of the skater is:
vk≈0.105m/s
The approximate recoil speed of the skater is 0.10m/s (in the opposite direction to the snowball).
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 3: Equilibrium of Forces, Motion of Connected Bodies and Pulley )
12 Videos
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 4: Friction )
10 Videos
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 1: I, Il & illrd Laws of Motion)
14 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
Similar Questions
Knowledge Check
A radioactive nucleus of mass number A, initially at rest, emits an α− particle with a speed v. What will be the recoil speed of the daughter nucleus ?
A2vA−4B2vA+4C4vA−4D4vA+4A uranium 238 nucleus, originally at rest, emits and α particle. The α particle travels with a speed of v m/s. What is the recoil speed of the residual necleus?
Av4m/sB−2v117m/sC−117v2m/sD4v238m/sA 10g bullet is short from a 5kg gun with a velocity of 400m/s. What is the speed of recoil of the gun?
A-0.8 m/sB80 m/sC0.4 m/sD20 m/s
Calculate the de-Broglie wavelength of a 0.20 kg ball moving with a speed of 15 m/s
View SolutionA 0.70 kg ball moving horizontally at 6.0 m/s strikes a vertical wall and rebounds with speed 3.5 m/s. What is the magnitude of the change in its linear momentum?
View SolutionA gun of mass 4 kg initially at rest fires a bullet of mass 4g with a speed of 50m/s as seen by an observer on ground. Find the impulse on bullet and recoil speed of the gun.
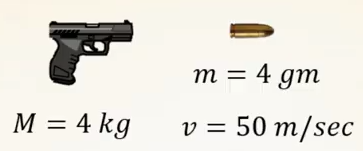
View SolutionA 2.5-kg ball and a 5.0-kg ball have an elastic collision. Before the collision, the 2.5-kg ball was at rest and the other ball had a speed of 3.5 m/s. What is the kinetic energy of the 2.5-kg ball after the collision?
View SolutionA 1580 kg car is traveling with a speed of 15.0 m/s. What is the magnitude of the horizontal net force that is required to bring the car to a halt in a distance of 50.0 m ?
View Solution
