A uniform chain of length / and mass mis hanging vertically from its ends A and B which are close together. At a given instant the end B is released. What is the tension at A when B has fallen a distance x (x<l)?
mg2[1+3xl]
mg[1+2xl]
mg2[1+xl]
mg2[1+4xl]
The correct Answer is:A
To find the tension at point A when end B of a uniform chain has fallen a distance x (where x<L), we can follow these steps:
Step 1: Understand the System
We have a uniform chain of length L and mass m hanging vertically. When the end B is released, it begins to fall under the influence of gravity. The tension at point A will depend on the mass of the chain that is still hanging and the dynamics of the falling chain.
Step 2: Determine the Mass of the Chain Still Hanging
When end B has fallen a distance x, the length of the chain that is still hanging from point A is L−x. The mass of this hanging portion can be calculated using the ratio of the lengths:
mhanging=mL(L−x)=m(1−xL)
Step 3: Calculate the Weight of the Hanging Portion
The weight of the hanging portion of the chain is given by:
W=mhanging⋅g=m(1−xL)g
Step 4: Consider the Dynamics of the Falling Chain
When end B falls a distance x, it accelerates due to gravity. The tension at point A must support the weight of the hanging portion of the chain and provide the necessary force to accelerate the chain.
Step 5: Apply Newton's Second Law
The net force acting on the hanging portion of the chain can be expressed as:
T−W=mhanging⋅a
where T is the tension at point A, W is the weight of the hanging portion, and a is the acceleration of the chain.
Step 6: Determine the Acceleration
Since the chain is falling freely, the acceleration a is equal to g. Thus, we can rewrite the equation as:
T−m(1−xL)g=m(1−xL)g
Step 7: Solve for Tension T
Rearranging the equation gives us:
T=2m(1−xL)g
Final Expression for Tension
The tension at point A when end B has fallen a distance x is:
T=2mg(1−xL)
We have a uniform chain of length L and mass m hanging vertically. When the end B is released, it begins to fall under the influence of gravity. The tension at point A will depend on the mass of the chain that is still hanging and the dynamics of the falling chain.
When end B has fallen a distance x, the length of the chain that is still hanging from point A is L−x. The mass of this hanging portion can be calculated using the ratio of the lengths:
mhanging=mL(L−x)=m(1−xL)
The weight of the hanging portion of the chain is given by:
W=mhanging⋅g=m(1−xL)g
When end B falls a distance x, it accelerates due to gravity. The tension at point A must support the weight of the hanging portion of the chain and provide the necessary force to accelerate the chain.
The net force acting on the hanging portion of the chain can be expressed as:
T−W=mhanging⋅a
where T is the tension at point A, W is the weight of the hanging portion, and a is the acceleration of the chain.
Since the chain is falling freely, the acceleration a is equal to g. Thus, we can rewrite the equation as:
T−m(1−xL)g=m(1−xL)g
Rearranging the equation gives us:
T=2m(1−xL)g
The tension at point A when end B has fallen a distance x is:
T=2mg(1−xL)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 4: Friction )
10 Videos
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 5: Circular Motion and Banking of Road )
7 Videos
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 2: Momentum, Law of Conservation of Momentum and Impulse)
15 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
Similar Questions
A very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
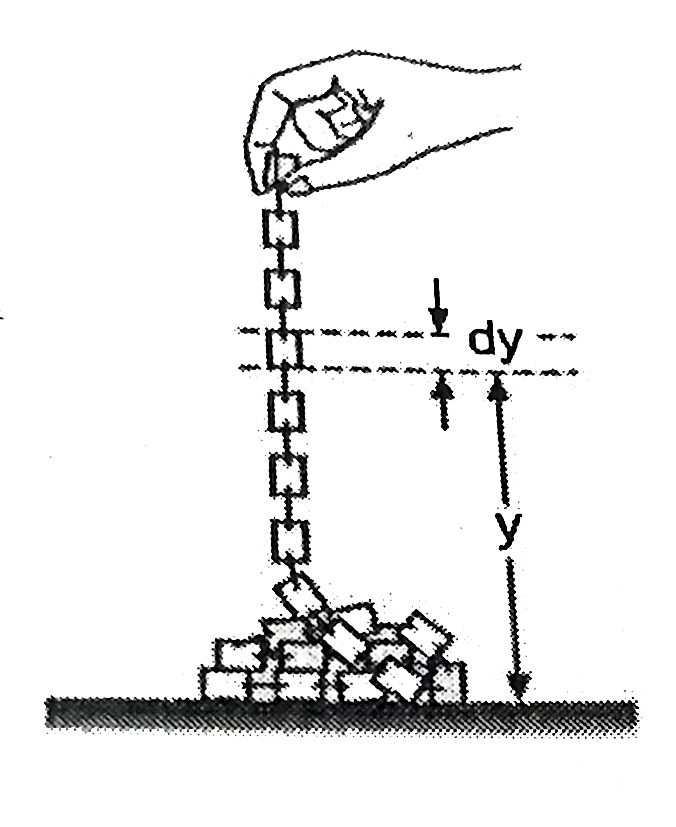
View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View Solution
Knowledge Check
A uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 A2√5g71B2√6g71C√3g71D2√21
A2√5g71B2√6g71C√3g71D2√21A string of length L and mass M hangs freely from a fixed point. Then the velocity of transverse waves along the string at a distance x from the free end is
A√gLB√gxCgLDgx
A very flexible unifrom chain of mass M and length L is suspended vertically so that its lower end just touches the surface of a table When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table Find the force exerted by the chain on the table at the moment when x part of chain has already rested on the table .
View SolutionA chain of length l and mass m lies in a pile on the floor. If its end A is raised vertically at a constant speed v0, express in terms of the length y of chain which is off the floor at any given instant.
(a) The magnitude of the force P applied to end A.
(b) Energy lost during the lifting of the chain.

View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
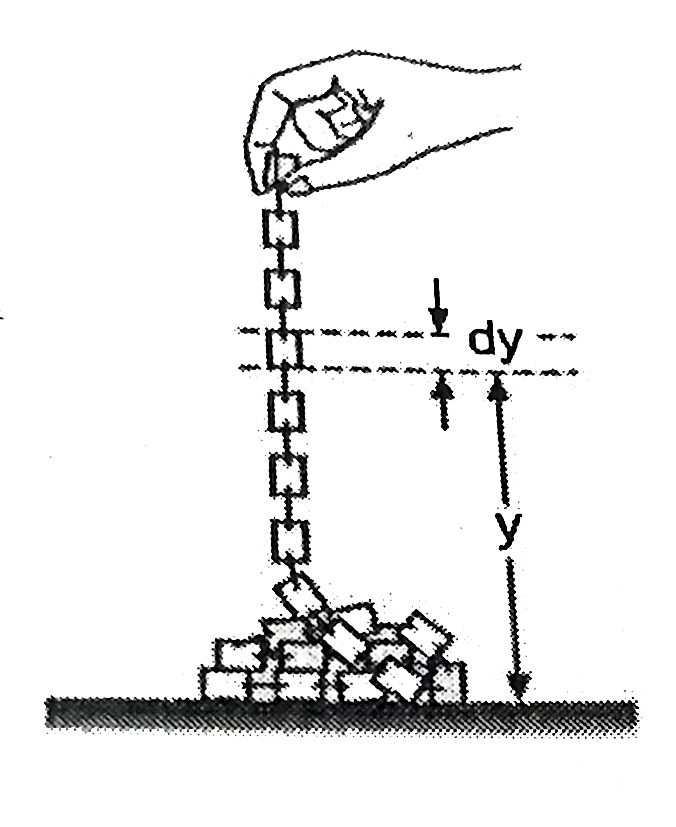
View SolutionA thin, uniform chain is hanging vertically and its bottom end is touching a table . The mass of the chain is m and its length is l . At the moment t=0, the chain is released. Calculate the force that the chain exerts on the table after t seconds.
View SolutionA rigid rod of length l but of negligible mass has heavy mass m attached to one end and is hinged freely at the upper end. It is inverted and then released. What is its speed at the lowest point and what is the tension in the suspension at that instant ? When the same is released from the horizontal position, at what angle from the vertical will the tension in the suspension equal the weight ?
[Hint : Consider conservation of energy and dynamics of circular motion]
View SolutionA chain of length L is supported at one end and is hanging vertically when it is released. All of the chain falls freely with acceleration g. The moment, the chain is released a ball is projected up with speed u from a point 2 L below the point of support. Find the interval of time in which the ball will cross through the entire chain.
View Solution
