Block A is moving with acceleration A along a frictionless horizontal surface. When a second block, B is placed on top of Block A the acceleration of the combined blocks drops to 1/5 the original value. What is the ratio of the mass of A to the mass of B?
5:1
1:4
3:1
2:1
The correct Answer is:B
To solve the problem, we need to analyze the situation using Newton's second law of motion. Let's break it down step by step.
Step 1: Understand the initial conditions
Block A is moving with an acceleration A on a frictionless surface. The force acting on Block A can be expressed as:
F=mA⋅A
where mA is the mass of Block A.
Step 2: Introduce Block B
When Block B is placed on top of Block A, the total mass of the system becomes mA+mB, where mB is the mass of Block B. The problem states that the acceleration of the combined blocks drops to A5.
Step 3: Write the equation for the combined system
The force acting on the combined system is still the same, and can be expressed as:
F=(mA+mB)⋅A5
Step 4: Set the equations equal to each other
Since the force remains constant, we can set the two expressions for force equal to each other:
mA⋅A=(mA+mB)⋅A5
Step 5: Simplify the equation
We can cancel A from both sides (since A≠0):
mA=(mA+mB)⋅15
Step 6: Multiply both sides by 5
Multiplying both sides by 5 gives us:
5mA=mA+mB
Step 7: Rearrange the equation
Rearranging the equation to isolate mB:
5mA−mA=mB
4mA=mB
Step 8: Find the ratio of the masses
Now, we can find the ratio of the mass of Block A to the mass of Block B:
mAmB=mA4mA=14
Conclusion
Thus, the ratio of the mass of Block A to the mass of Block B is:
mAmB=14
---
Block A is moving with an acceleration A on a frictionless surface. The force acting on Block A can be expressed as:
F=mA⋅A
where mA is the mass of Block A.
When Block B is placed on top of Block A, the total mass of the system becomes mA+mB, where mB is the mass of Block B. The problem states that the acceleration of the combined blocks drops to A5.
The force acting on the combined system is still the same, and can be expressed as:
F=(mA+mB)⋅A5
Since the force remains constant, we can set the two expressions for force equal to each other:
mA⋅A=(mA+mB)⋅A5
We can cancel A from both sides (since A≠0):
mA=(mA+mB)⋅15
Multiplying both sides by 5 gives us:
5mA=mA+mB
Rearranging the equation to isolate mB:
5mA−mA=mB
4mA=mB
Now, we can find the ratio of the mass of Block A to the mass of Block B:
mAmB=mA4mA=14
Thus, the ratio of the mass of Block A to the mass of Block B is:
mAmB=14
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 4: Friction )
10 Videos
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 5: Circular Motion and Banking of Road )
7 Videos
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 2: Momentum, Law of Conservation of Momentum and Impulse)
15 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
Similar Questions
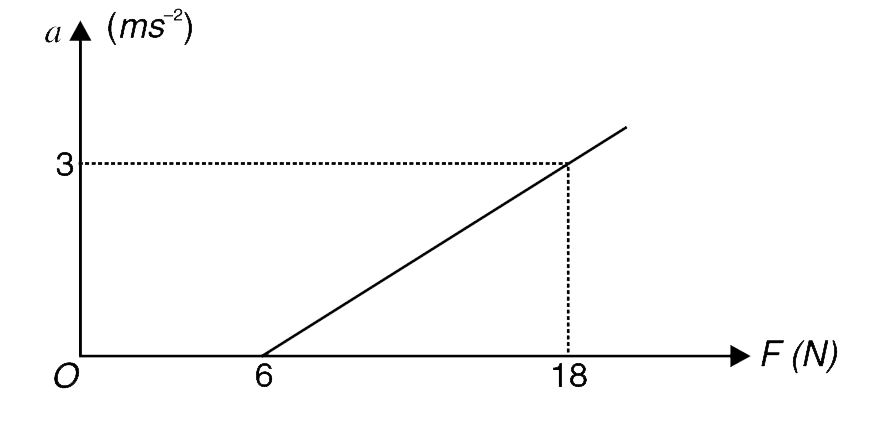
A block rests on a horizontal surface. A horizontal force F is applied to the block. The acceleration (a) produced in the block as a function of applied force (F) has been plotted in a graph (see figure). Find the mass of the block.
View SolutionTwo blocks are connected by a string that passes over a pulley of radius R and moment of inertia I. The block of mass m1 sides on a frictionless, horizontal surface, the block of mass m2 is suspended from the string. Find the acceleration a of the blocks and the tension T1 and T2 assuming that the string does not slip on the pulley.

View Solution
Knowledge Check
A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of theseA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is
 A1.0kgB0.1kgC2.0kgD0.2kg
A1.0kgB0.1kgC2.0kgD0.2kgTwo forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?
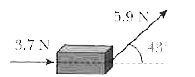 A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2
A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . A force P is applied to the other end of the rope . (a) Find the acceleration of the block and the rope . (b) Find the force that the rope exerts on the block M in terms of P, M and m .
View SolutionIf block B moves towards right with acceleration b, find the net acceleration of block A.

View SolutionFind the acceleration of the block of mass m. Assume pulleys are massless and frictionless.

View SolutionA block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
What is the magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom ?
View Solution
